TP2: Metropolis-Hastings
Metropolis-Hastings en 1D
El algoritmo de Metropolis-Hastings (MH) permite generar muestras (pseudo-)aleatorias a partir de una distribución de probabilidad \(P\) que no necesariamente pertence a una familia de distribuciones conocida. El único requisito es que se pueda evaluar la función de densidad (o de masa de probabilidad) \(p^*(\theta)\) en cualquier valor de \(\theta\), incluso cuando \(p^*(\theta)\) sea impropia (es decir, incluso aunque sea desconocida la constante de normalización que hace que la integral en el soporte de la función sea igual a uno).
- Escriba una función que implemente el algoritmo de Metropolis-Hastings para tomar muestras de una distribución de probabilidad unidimensional a partir de su función de densidad. Separe en funciones cada uno de los pasos del procedimiento. Otorgue flexibilidad al algoritmo permitiendo elegir entre un punto de inicio arbitrario o al azar y utilizar distribuciones de propuesta de transición arbitrarias (por defecto, se utiliza una distribución normal estándar).
Distribución de Kumaraswamy
La distribución de Kumaraswamy es una distribución de probabilidad continua que se utiliza para modelar variables aleatorias con soporte en el intervalo \((0, 1)\). Si bien graficamente la forma de su función de densidad puede hacernos recordar a la distribución beta, vale mencionar que la distribución de Kumaraswamy resulta en una expresión matemática cuyo cómputo es más sencillo:
\[ \begin{array}{lr} p(x \mid a, b) = a b x ^ {a - 1} (1 - x ^ a)^{b - 1} & \text{con } a, b > 0 \end{array} \]
Grafique la función de densidad de la distribución de Kumaraswamy para 5 combinaciones de los parámetros \(a\) y \(b\) que crea convenientes. Concluya sobre la utilidad que puede tener en la estadística bayesiana.
Utilizando la función construida en el punto 1, obtenga 5000 muestras de una distribución de Kumaraswamy con parámetros \(a=6\) y \(b=2\). Utilice una distribución de propuesta beta. Tenga en cuenta que la misma se puede parametrizar según media \(\mu = \alpha / (\alpha + \beta)\) y concentración \(\kappa = \alpha + \beta\).
Compare las cadenas obtenidas al utilizar tres grados de concentración distintos en la distribución de propuesta. Calcule la tasa de aceptación. Compare utilizando histogramas y funciones de autocorrelación (puede utilizar la función
acfo escribir una función propia). Para elegir el punto inicial del algoritmo de MH, obtenga un valor aleatorio de una distribución conocida que sea conveniente.Utilizando cada una de las cadenas anteriores, compute la media de la distribución y los percentiles 5 y 95 de \(X\) y de \(\mathrm{logit}(X)\).
Metropolis-Hastings en 2D
Como veremos en esta sección del trabajo práctico, la verdadera utilidad del algoritmo de Metropolis-Hastings se aprecia cuando se obtienen muestras de distribuciones en más de una dimensión, incluso cuando no se conoce la constante de normalización. Paradójicamente, los ejemplos trabajados a continuación también serán los que nos permitirán advertir sus limitaciones y motivarán la búsqueda de mejores alternativas.
Normal multivariada
La distribución normal multivariada es la generalización de la distribución normal univariada a múltiples dimensiones (o mejor dicho, el caso en una dimensión es un caso particular de la distribución en múltiples dimensiones). La función de densidad de la distribución normal en \(k\) dimensiones es:
\[ p(\boldsymbol{x} \mid \boldsymbol{\mu}, \boldsymbol{\Sigma}) = \frac{1}{(2\pi)^{k/2} |\boldsymbol{\Sigma}|^{1/2}} \exp\left(-\frac{1}{2} (\boldsymbol{x} - \boldsymbol{\mu})^T \boldsymbol{\Sigma}^{-1} (\boldsymbol{x} - \boldsymbol{\mu})\right) \]
donde \(\boldsymbol{\mu}\) es el vector de medias y \(\boldsymbol{\Sigma}\) la matriz de covarianza.
Escriba una función que implemente el algoritmo de Metropolis-Hastings para tomar muestras de una función de probabilidad bivariada dada. Separe en funciones cada una de los pasos del algoritmo. La probabilidad de salto será normal bivariada de matriz de covarianza variable (utilizar para ello la función
rmvnormdel paquete{mvtnorm}). Otorgue flexibilidad al algoritmo haciendo que reciba como argumento la matriz de covarianza de la probabilidad de transición.Utilice la función escrita en el punto anterior para obtenga muestras de una distribución normal bivariada con media \(\boldsymbol{\mu}^*\) y matriz de covarianza \(\boldsymbol{\Sigma}^*\). Determine una matriz de covarianza que crea conveniente para la distribución de propuesta. Justifique su decisión y valide la bondad del método mediante el uso de traceplots y las estadísticas que crea adecuadas.
\[ \begin{array}{lr} \boldsymbol{\mu}^* = \begin{bmatrix} 0.4 \\ 0.75 \end{bmatrix} & \boldsymbol{\Sigma}^* = \begin{bmatrix} 1.35 & 0.4 \\ 0.4 & 2.4 \end{bmatrix} \end{array} \]
Estime las siguientes probabilidades utilizando las muestras obtenidas:
- \(\mathrm{Pr}(X_1 > 1, X_2 < 0)\)
- \(\mathrm{Pr}(X_1 > 1, X_2 > 2)\)
- \(\mathrm{Pr}(X_1 > 0.4, X_2 > 0.75)\)
Luego, calcule esas mismas probabilidades mediante algún método que crea conveniente (función de distribución, integración manual, integración numérica, monte carlo, etc.), y compare los resultados con los obtenidos en base a las muestras seleccionadas con MH y concluya.
Función de Rosenbrock
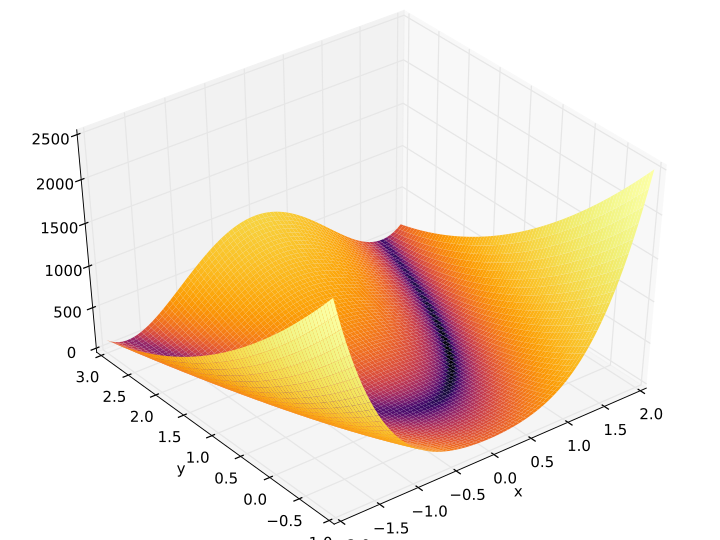
La función de Rosenbrock, a veces llamada el “valle de Rosenbrock”, y comunmente conocida como la “banana de Rosenbrock” 🍌, es una función matemática utilizada frecuentemente como un problema de optimización y prueba para algoritmos de optimización numérica.
La función está definida por: \[ f(x, y) = (a - x) ^ 2 + b(y - x^2) ^ 2 \]
y cuenta con un mínimo global en \((x, y) = (a, a^2)\), que satisface \(f(a, a^2) = 0\).
Debido a su forma peculiar, la función de Rosenbrock presenta desafíos particulares para los algoritmos de optimización, ya que tiene un valle largo y estrecho en el que la convergencia puede ser lenta.
Esta forma de banana popularizada por Rosenbrock es también muy conocida en el campo de la estadística bayesiana, ya que en ciertos escenarios, la densidad del posterior toma una forma que definitivamente se asemeja a la banana de Rosenbrock. Un ejemplo de este fenómeno es la función \(p^*\):
\[ p^*(x_1, x_2 \mid a, b) = \exp \left\{-\left[(a - x_1) ^ 2 + b(x_2 - x_1^2) ^ 2\right] \right\} \]
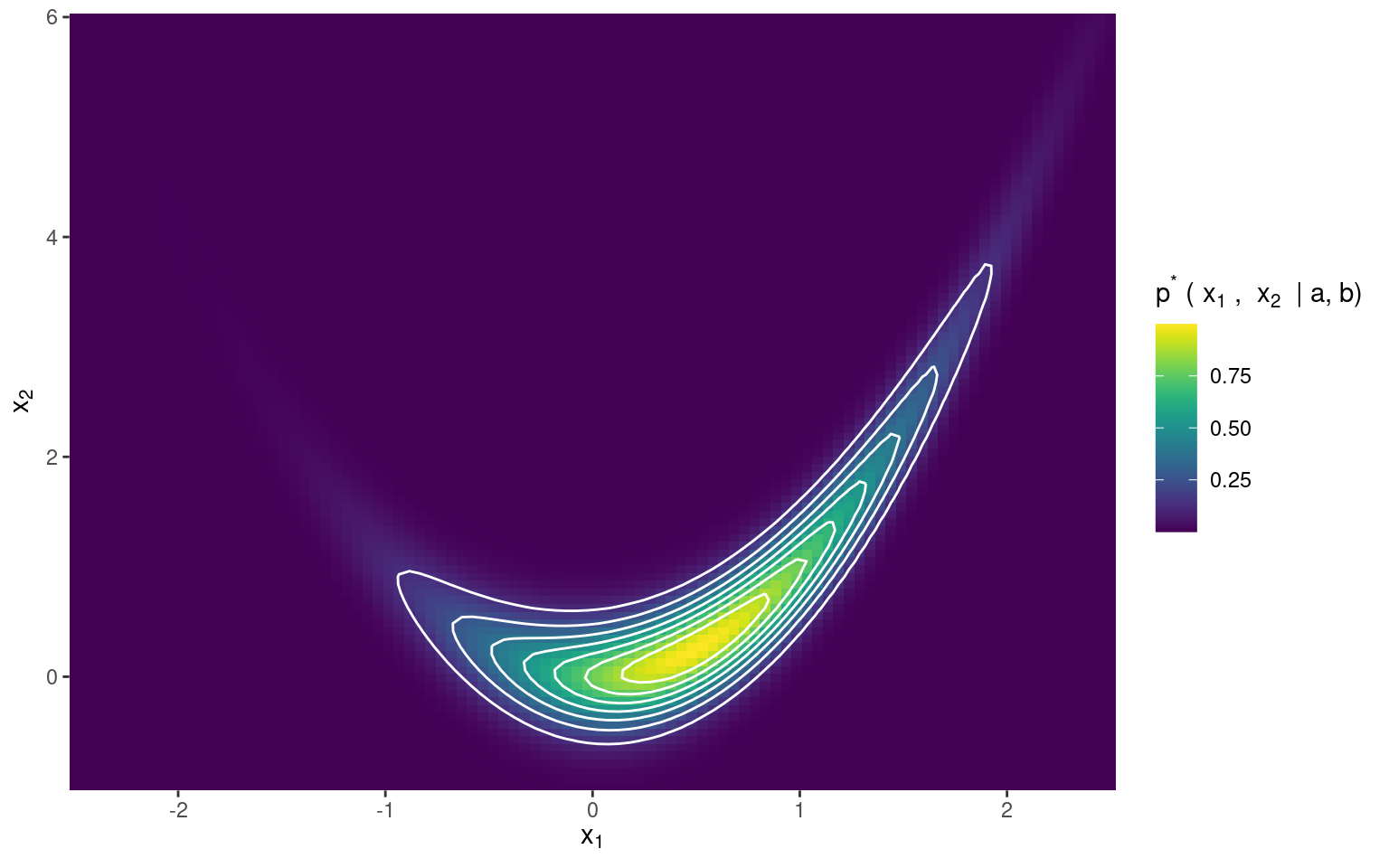
Obtenga muestras de la distribución a posteriori determinada por \(p^*\) con \(a=0.5\) y \(b=5\) utlizando la función implementada en el punto 6. Utilice tres matrices de covarianza distintas para la distribución de propuesta. En al menos dos de los casos, compare las trayectorias seguidas por las cadenas en el proceso de muestreo. Y en todos los casos, calcule la probabilidad de aceptación y muestre la función de autocorrelación.
Utilizando el conjunto de muestras que crea mas conveniente, estime las siguientes probabilidades:
- \(\mathrm{Pr}(0 < X_1 < 1, 0 < X_2 < 1)\)
- \(\mathrm{Pr}(-1 < X_1 < 0, 0 < X_2 < 1)\)
- \(\mathrm{Pr}(1 < X_1 < 2, 2 < X_2 < 3)\)
Finalmente, calcule las mismas probabilidades utilizando un método de su elección (integración manual, integración numérica, método de la grilla, etc.), compare los resultados y concluya sobre lo observado en este experimento en particular y sobre la utilidad del algoritmo de Metropolis-Hastings en general.