01 - Los ositos de Pagani

Este script fue utilizado en la primer clase de práctica en el laboratorio para mostrar como resolver el ejercicio de los ositos utilizando código.

library(ggplot2)
library(patchwork)

En base al prior elicitado grupalmente en clase:

# Determinar grilla de puntos
pi_grid <- seq(0, 1, length.out = 11)
print(pi_grid)
 [1] 0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0
# Especificar prior
# Tenemos $100 y los dividimos en los diferentes valores de "pi"
prior_ <- c(0, 5, 20, 50, 20, 5, 0, 0, 0, 0, 0)
prior <- prior_ / sum(prior_)

# Recolectar datos
cantidad_de_gomitas <- 10 # n
cantidad_de_gomitas_amarillas <- 6 # y

# Calcular verosimilitud para cada valor de "pi" en la grilla
likelihood <- dbinom(
  cantidad_de_gomitas_amarillas, 
  cantidad_de_gomitas, 
  pi_grid
)

# Obtener posterior
posterior_ <- prior * likelihood
posterior <- posterior_ / sum(posterior_) # normalización

# Graficar prior 
plt_prior <- data.frame(x = pi_grid, y = prior) |>
  ggplot() +
  geom_segment(aes(x = x, xend = x, y = 0, yend = y), linewidth = 0.8) +
  geom_point(aes(x = x, y = y), size = 2.4) +
  scale_x_continuous(breaks = pi_grid) +
  labs(
    x = expression(pi), 
    y = expression(p ~ "(" ~ pi ~ ")"), 
    title = "Distribución a priori"
  )

# Graficar verosimilitud
plt_likelihood <- data.frame(x = pi_grid, y = likelihood) |>
  ggplot() +
  geom_segment(aes(x = x, xend = x, y = 0, yend = y), linewidth = 0.8) +
  geom_point(aes(x = x, y = y), size = 2.4) +
  scale_x_continuous(breaks = pi_grid) +
  labs(
    x = expression(pi), 
    y = expression(p ~ "(y | " ~ pi ~ ")"), 
    title = "Función de verosimilitud"
  )

# Graficar posterior
plt_posterior <- data.frame(x = pi_grid, y = posterior) |>
  ggplot() +
  geom_segment(aes(x = x, xend = x, y = 0, yend = y), linewidth = 0.8) +
  geom_point(aes(x = x, y = y), size = 2.4) +
  scale_x_continuous(breaks = pi_grid) +
  labs(
    x = expression(pi), 
    y = expression(p ~ "(" ~ pi ~ " | y)"), 
    title = "Distribución a posteriori"
  )

# Concatenar graficos
plt_prior | plt_likelihood | plt_posterior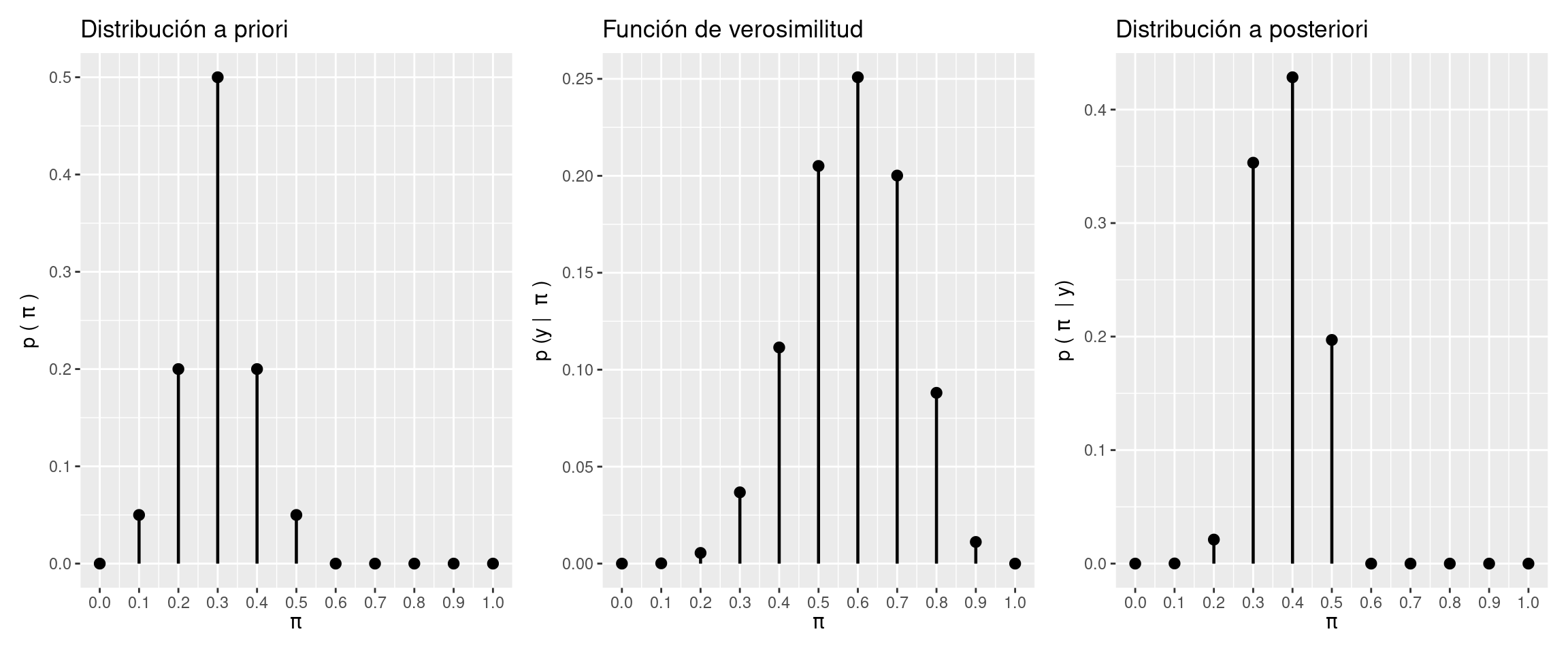

En base a un prior beta:

# Determinar grilla de puntos
pi_grid <- seq(0, 1, length.out = 100)

# Obtener prior
prior_ <- dbeta(pi_grid, 3, 7)
prior <- prior_ / sum(prior_)

# Calcular verosimilitud para cada valor de "pi"
likelihood <- dbinom(
  cantidad_de_gomitas_amarillas, 
  cantidad_de_gomitas, 
  pi_grid
)

# Obtener posterior 
posterior_ <- prior * likelihood
posterior <- posterior_ / sum(posterior_)

# Graficar prior 
plt_prior <- data.frame(x = pi_grid, y = prior) |>
  ggplot() +
  geom_line(aes(x = x, y = y)) +
  labs(
    x = expression(pi), 
    y = expression(p ~ "(" ~ pi ~ ")"), 
    title = "Distribución a priori"
  )

# Graficar verosimilitud
plt_likelihood <- data.frame(x = pi_grid, y = likelihood) |>
  ggplot() +
  geom_line(aes(x = x, y = y)) +
  labs(
    x = expression(pi), 
    y = expression(p ~ "(y | " ~ pi ~ ")"), 
    title = "Función de verosimilitud"
  )

# Graficar posterior
plt_posterior <- data.frame(x = pi_grid, y = posterior) |>
  ggplot() +
  geom_line(aes(x = x, y = y)) +
  labs(
    x = expression(pi), 
    y = expression(p ~ "(" ~ pi ~ " | y)"), 
    title = "Distribución a posteriori"
  )

# Concatenar graficos
plt_prior | plt_likelihood | plt_posterior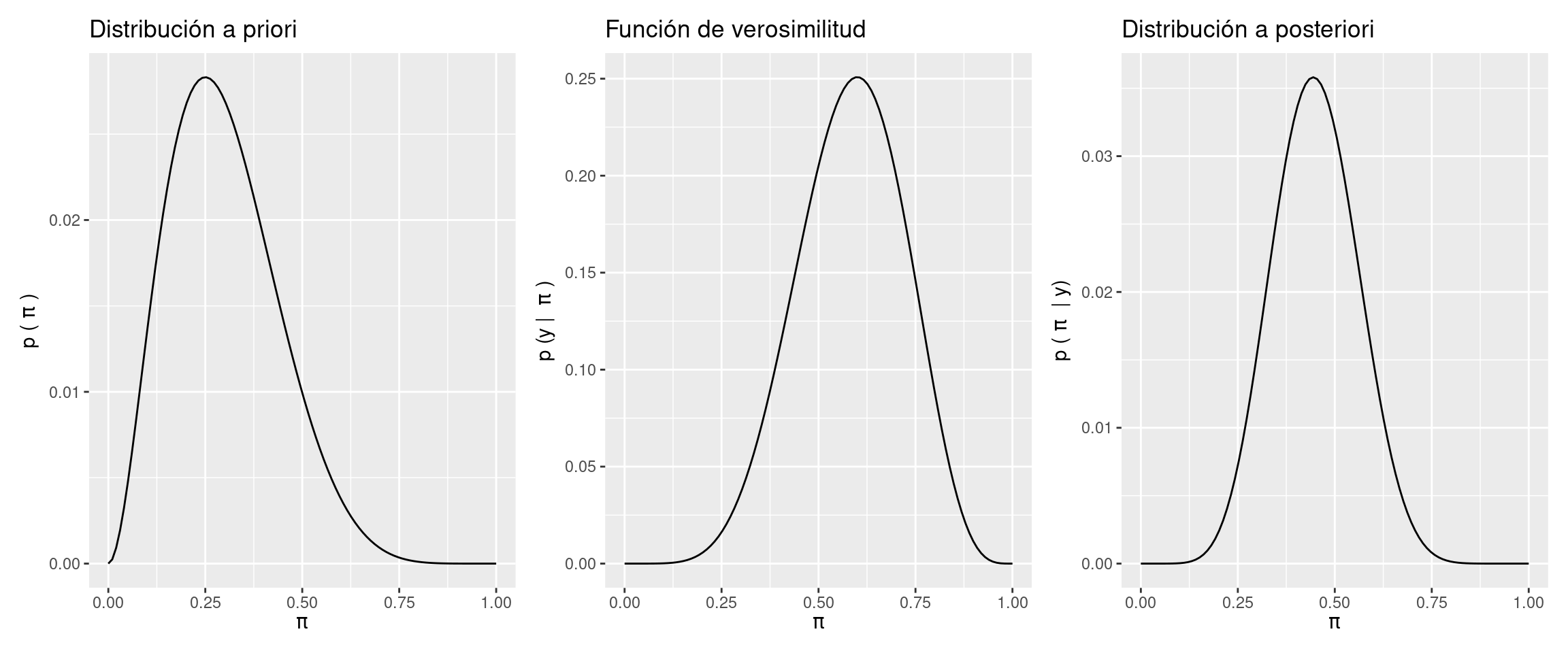

Preguntas