library(ggplot2)
# Valores observados de "Y"
y <- c(64, 13, 33, 18, 30, 20)
# Altura de la densidad a priori uniforme
prior <- rep(1 / 100, 400)
# Grilla con los valorse de lambda
lambda_grid <- seq(0, 100, length.out = 400)02 - ¡Ostras! ¡Estoy haciendo inferencia bayesiana!
El siguiente programa muestra diferentes alternativas para obtener la densidad de la distribución a posteriori en el ejercicio ¡Ostras! ¡Estoy haciendo inferencia bayesiana! de la Práctica 1.
Tener presente:
\[ \begin{aligned} p(\boldsymbol{y} \mid \lambda) &= \prod_{i=1}^n p(y_i \mid \lambda) \\ p(\boldsymbol{y} \mid \lambda) &= \prod_{i=1}^n {\frac{e^{-\lambda}\lambda^{y_i}}{y_i!}} \\ & = \frac{e^{-n\lambda}\lambda^{\sum_i y_i}}{\prod_{i=1}^{n}{y_i!}} \\ \log p(\boldsymbol{y} \mid \lambda) &= \sum_{i=1}^{n} p(y_i \mid \lambda) \end{aligned} \]
Opción 1: Replicar la fórmula de la función de verosimilitud en una función de R
f_likelihood <- function(lambda, y_vector) {
n <- length(y_vector)
y_suma <- sum(y_vector)
denominador <- prod(factorial(y_vector))
(exp(- n * lambda) * lambda ^ y_suma) / denominador
}
likelihood <- f_likelihood(lambda_grid, y)
posterior_ <- prior * likelihood
posterior_ [1] 0.000000e+00 8.341450e-313 7.104056e-260 3.488800e-229 1.344921e-207
[6] 5.316241e-191 1.468223e-177 2.693061e-166 1.258167e-156 3.562976e-148
[11] 1.105533e-140 5.733178e-134 6.787109e-128 2.324156e-122 2.767353e-117
[16] 1.325696e-112 2.873971e-108 3.104267e-104 1.809183e-100 6.081954e-97
[21] 1.247863e-93 1.639788e-90 1.438521e-87 8.732918e-85 3.785569e-82
[26] 1.204418e-79 2.881624e-77 5.297329e-75 7.627146e-73 8.749872e-71
[31] 8.122076e-69 6.185727e-67 3.914092e-65 2.081334e-63 9.397953e-62
[36] 3.637672e-60 1.217538e-58 3.551973e-57 9.098475e-56 2.060222e-54
[41] 4.149713e-53 7.478107e-52 1.212173e-50 1.776239e-49 2.363842e-48
[46] 2.869426e-47 3.189974e-46 3.260149e-45 3.073864e-44 2.682700e-43
[51] 2.173984e-42 1.640637e-41 1.156224e-40 7.629166e-40 4.724840e-39
[56] 2.752848e-38 1.512230e-37 7.848722e-37 3.856409e-36 1.797148e-35
[61] 7.957451e-35 3.353418e-34 1.347173e-33 5.167090e-33 1.894912e-32
[66] 6.653603e-32 2.239884e-31 7.238448e-31 2.248240e-30 6.719236e-30
[71] 1.934454e-29 5.370553e-29 1.439272e-28 3.726947e-28 9.333742e-28
[76] 2.262769e-27 5.314719e-27 1.210418e-26 2.675170e-26 5.741957e-26
[81] 1.197791e-25 2.430089e-25 4.798220e-25 9.226574e-25 1.728934e-24
[86] 3.159075e-24 5.631721e-24 9.800977e-24 1.666033e-23 2.767673e-23
[91] 4.495581e-23 7.143525e-23 1.110973e-22 1.691846e-22 2.523943e-22
[96] 3.690191e-22 5.289958e-22 7.438185e-22 1.026279e-21 1.389998e-21
[101] 1.848737e-21 2.415490e-21 3.101393e-21 3.914514e-21 4.858608e-21
[106] 5.931961e-21 7.126440e-21 8.426877e-21 9.810887e-21 1.124921e-20
[111] 1.270659e-20 1.414317e-20 1.551637e-20 1.678304e-20 1.790181e-20
[116] 1.883539e-20 1.955269e-20 2.003058e-20 2.025504e-20 2.022183e-20
[121] 1.993649e-20 1.941370e-20 1.867617e-20 1.775307e-20 1.667820e-20
[126] 1.548806e-20 1.421993e-20 1.291006e-20 1.159221e-20 1.029641e-20
[131] 9.048144e-21 7.867903e-21 6.771014e-21 5.767820e-21 4.864064e-21
[136] 4.061454e-21 3.358320e-21 2.750318e-21 2.231130e-21 1.793113e-21
[141] 1.427871e-21 1.126747e-21 8.812014e-22 6.831092e-22 5.249581e-22
[146] 3.999734e-22 3.021764e-22 2.263932e-22 1.682243e-22 1.239895e-22
[151] 9.065646e-23 6.576228e-23 4.733305e-23 3.380696e-23 2.396323e-23
[156] 1.685873e-23 1.177299e-23 8.161536e-24 5.617212e-24 3.838602e-24
[161] 2.604758e-24 1.755262e-24 1.174720e-24 7.808739e-25 5.156059e-25
[166] 3.382054e-25 2.203960e-25 1.426992e-25 9.180523e-26 5.869137e-26
[171] 3.728846e-26 2.354505e-26 1.477683e-26 9.218273e-27 5.716563e-27
[176] 3.524253e-27 2.160105e-27 1.316397e-27 7.976853e-28 4.806581e-28
[181] 2.880237e-28 1.716462e-28 1.017374e-28 5.997816e-29 3.517201e-29
[186] 2.051719e-29 1.190639e-29 6.873967e-30 3.948428e-30 2.256596e-30
[191] 1.283274e-30 7.261782e-31 4.089292e-31 2.291691e-31 1.278170e-31
[196] 7.095239e-32 3.920239e-32 2.155985e-32 1.180285e-32 6.432150e-33
[201] 3.489582e-33 1.884768e-33 1.013513e-33 5.426324e-34 2.892720e-34
[206] 1.535499e-34 8.116204e-35 4.272035e-35 2.239301e-35 1.168970e-35
[211] 6.077494e-36 3.146971e-36 1.623022e-36 8.337508e-37 4.266228e-37
[216] 2.174523e-37 Inf Inf Inf Inf
[221] Inf Inf Inf Inf Inf
[226] Inf Inf Inf Inf Inf
[231] Inf Inf Inf Inf Inf
[236] Inf Inf Inf Inf Inf
[241] Inf Inf Inf Inf Inf
[246] Inf Inf Inf Inf Inf
[251] Inf Inf Inf Inf Inf
[256] Inf Inf Inf Inf Inf
[261] Inf Inf Inf Inf Inf
[266] Inf Inf Inf Inf Inf
[271] Inf Inf Inf Inf Inf
[276] Inf Inf Inf Inf Inf
[281] Inf Inf Inf Inf Inf
[286] Inf Inf Inf Inf Inf
[291] Inf Inf Inf Inf Inf
[296] Inf Inf Inf Inf Inf
[301] Inf Inf Inf Inf Inf
[306] Inf Inf Inf Inf Inf
[311] Inf Inf Inf Inf Inf
[316] Inf Inf Inf Inf Inf
[321] Inf Inf Inf Inf Inf
[326] Inf Inf Inf Inf Inf
[331] Inf Inf Inf Inf Inf
[336] Inf Inf Inf Inf Inf
[341] Inf Inf Inf Inf Inf
[346] Inf Inf Inf Inf Inf
[351] Inf Inf Inf Inf Inf
[356] Inf Inf Inf Inf Inf
[361] Inf Inf Inf Inf Inf
[366] Inf Inf Inf Inf Inf
[371] Inf Inf Inf Inf Inf
[376] Inf Inf Inf Inf Inf
[381] Inf Inf Inf Inf Inf
[386] Inf Inf Inf Inf Inf
[391] Inf Inf Inf Inf Inf
[396] Inf Inf Inf Inf InfLa densidad a posteriori no normalizada resulta Inf en algunos casos. Esto indica que el computo no es estable. Veamos otras alternativas.
Opción 2: Utilizar la funcion dpois de R para evaluar la función de masa de probabilidad en cada observación y luego obtener la función de verosimilitud multiplicando estos resultados.
f_likelihood <- function(lambda, y_vector) {
output <- numeric(length(lambda))
for (i in seq_along(output)) {
output[i] <- prod(dpois(y_vector, lambda[i]))
}
output
}
likelihood <- f_likelihood(lambda_grid, y)
posterior_ <- prior * likelihood
area <- integrate(f_likelihood, lower = 0, upper = 100, y_vector = y)$value
posterior <- posterior_ / area
df <- data.frame(
grupo = factor(
rep(c("prior", "likelihood", "posterior"), each = 400),
levels = c("prior", "likelihood", "posterior"),
ordered = TRUE
),
lambda = rep(lambda_grid, 3),
valor = c(prior, likelihood, posterior)
)
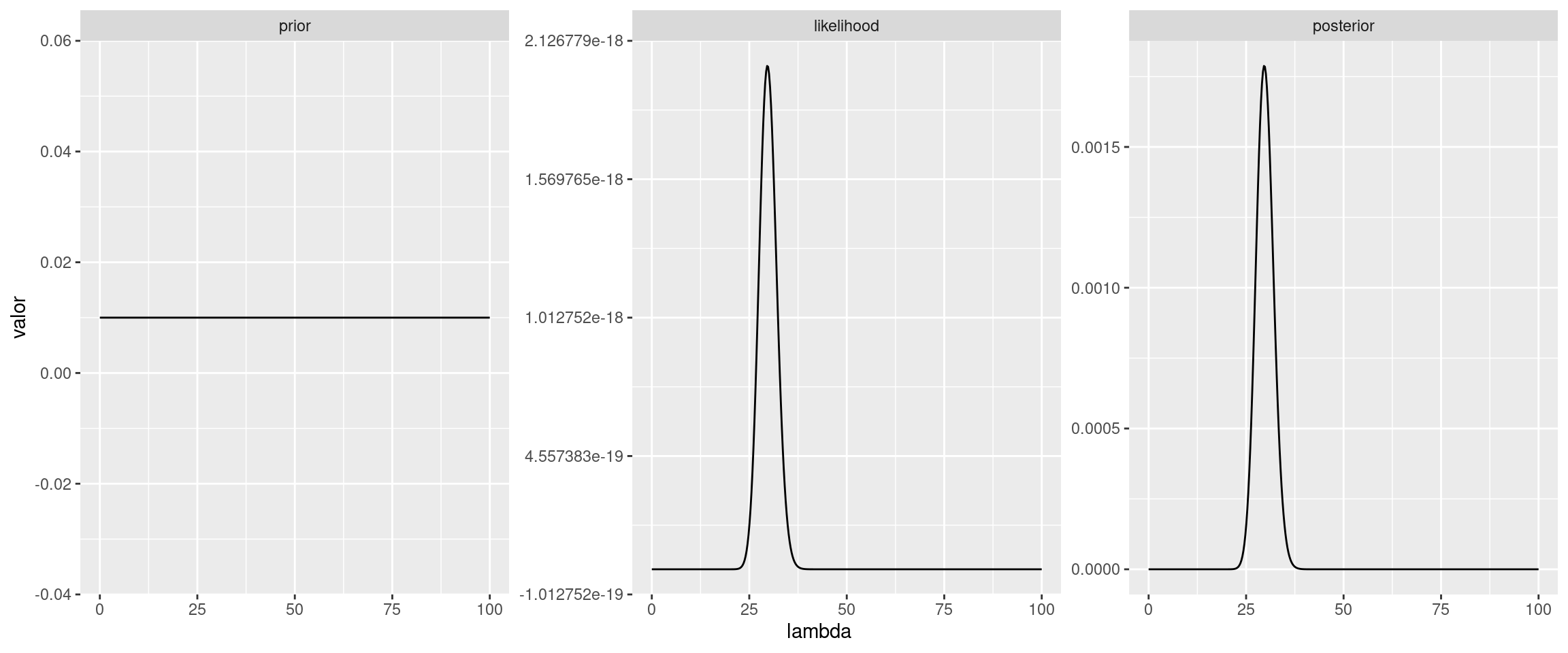
ggplot(df) +
geom_line(aes(x = lambda, y = valor)) +
facet_wrap(~ grupo, scales = "free_y") 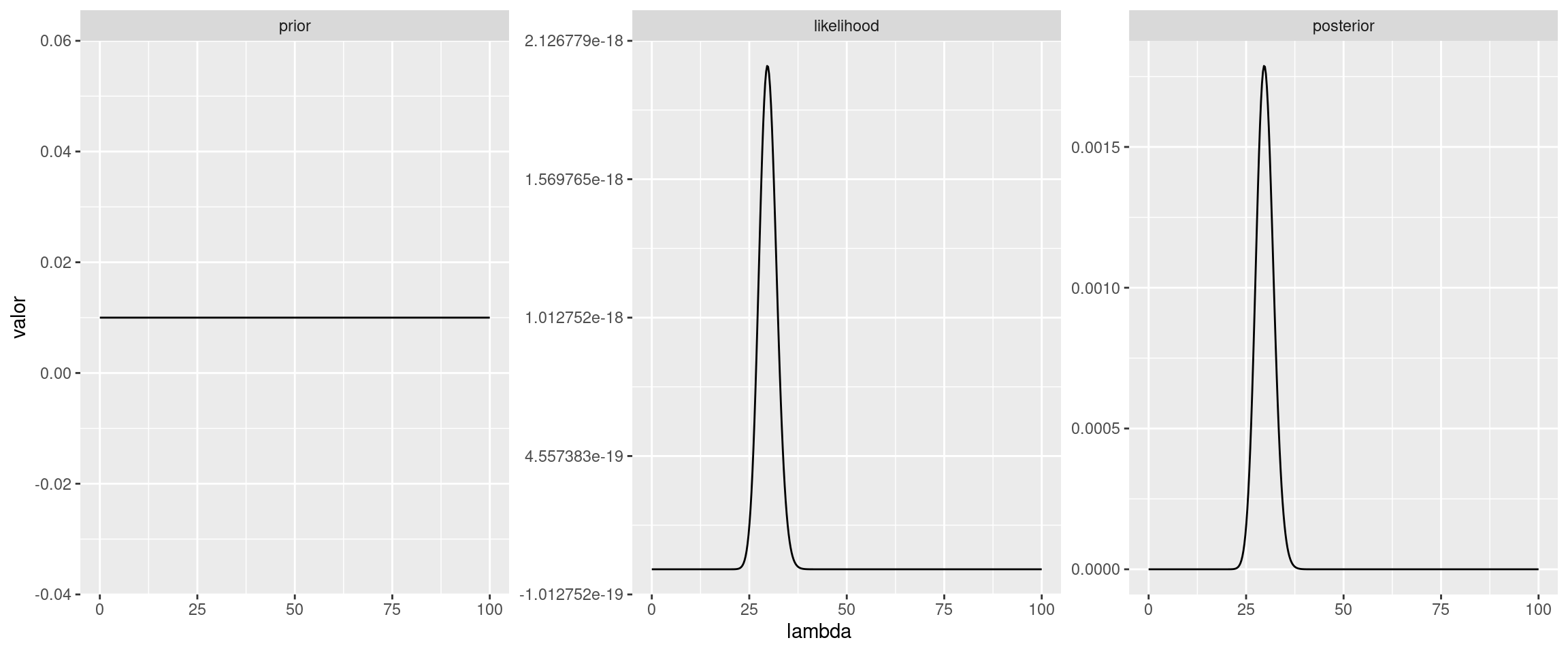
Opción 2: Utilizar la funcion dpois de R, pero hacer cuentas en escalas logaritmica
f_likelihood <- function(lambda, y_vector) {
output <- numeric(length(lambda))
for (i in seq_along(output)) {
# El producto se transforma en suma
output[i] <- sum(dpois(y_vector, lambda[i], log = TRUE))
}
# Volver a la escala original
exp(output)
}
likelihood <- f_likelihood(lambda_grid, y)
posterior_ <- prior * likelihood
area <- integrate(f_likelihood, lower = 0, upper = 100, y_vector = y)$value
posterior <- posterior_ / area
df <- data.frame(
grupo = factor(
rep(c("prior", "likelihood", "posterior"), each = 400),
levels = c("prior", "likelihood", "posterior"),
ordered = TRUE
),
lambda = rep(lambda_grid, 3),
valor = c(prior, likelihood, posterior)
)
ggplot(df) +
geom_line(aes(x = lambda, y = valor)) +
facet_wrap(~ grupo, scales = "free_y")