library(dplyr)
library(ggdist)
library(ggplot2)
library(rstan)
library(tidybayes)
# Colores para las visualizaciones
colores <- c(
"#107591",
"#00c0bf",
"#f69a48",
"#fdcd49",
"#8da798",
"#a19368",
"#525252",
"#a6761d",
"#7035b7",
"#cf166e"
)16 - Regresión logística con{RStan}
En este programa se muestra código de R que se puede utilizar con el ejercicio Intención de voto de la Práctica 5.
La variable respuesta \(Y\) se define:
\[ \begin{split}Y_i = \left\{ \begin{array}{ll} 1 & \text{si la persona } i \text{ vota al candidato A} \\ 0 & \text{si la persona } i \text{ vota al candidato B} \end{array} \right.\end{split} \]
Se trabaja con los siguientes dos modelos:
\[ \begin{array}{lc} \mathcal{M}_1 & \begin{aligned} Y_i \mid \pi_i &\sim \text{Bernoulli}(\pi_i) \\ \text{logit}(\pi_i) &= \beta_0 + \beta_1 \text{edad}_i \\ \end{aligned} \\ \\ \mathcal{M}_2 & \begin{aligned} Y_i \mid \pi_i &\sim \text{Bernoulli}(\pi_i) \\ \text{logit}(\pi_i) &= \beta_{0, j[i]} + \beta_{1, j[i]} \text{edad}_i \\ \end{aligned} \end{array} \]
donde \(j = 1, 2, 3\) indexa a los diferentes partidos.
Leemos los datos desde el repositorio de la materia:
ruta <- "https://raw.githubusercontent.com/estadisticaunr/estadistica-bayesiana/main/datos/elecciones.csv"
datos <- readr::read_csv(ruta)
print(nrow(datos))
head(datos)[1] 373
# A tibble: 6 × 3
voto edad partido
<chr> <dbl> <chr>
1 candidato A 56 azul
2 candidato B 65 rojo
3 candidato A 80 azul
4 candidato B 38 rojo
5 candidato B 60 rojo
6 candidato B 35 azul Tenemos 373 observaciones y 3 variables: voto, edad y partido. La primera es binaria, la segunda es numérica y la tercera es categórica.
La variable respuesta es voto. Veamos cuantas personas votan por cada candidato.
table(datos$voto) # Frecuencias
prop.table(table(datos$voto)) # Frecuencias relativas
candidato A candidato B
215 158
candidato A candidato B
0.5764075 0.4235925 La mayor parte de las personas, el 57.6%, dicen votar por el candidato A.
Por otro lado, tenemos las variables explicativas. Una de ellas es el partido político con el que se identifica la persona que responde (partido). Veamos su distribución:
table(datos$partido)
prop.table(table(datos$partido))
azul rojo verde
176 81 116
azul rojo verde
0.4718499 0.2171582 0.3109920 El grupo mayoritario es el de las personas que se identifican con el partido azul (47.2%), luego le sigue el partido verde (31.1%) y finalmente el partido rojo (21.7%).
Para comenzar a entender la asociación entre el partido y voto, podemos explorar la distribución condicional de voto para los diferentes niveles de la variable partido.
Un primer intento es el siguiente, basado como hasta ahora en table() y prop.table():
table(datos$partido, datos$voto)
prop.table(table(datos$partido, datos$voto))
candidato A candidato B
azul 159 17
rojo 5 76
verde 51 65
candidato A candidato B
azul 0.42627346 0.04557641
rojo 0.01340483 0.20375335
verde 0.13672922 0.17426273Pero esto nos devuelve la distribución conjunta. Para obtener la condicional debemos usar el argumento margin de prop.table() que indica el margen por el cual normalizar los conteos. Usamos margin = 1 porque queremos dividir los conteos de la tabla por los totales de las filas.
prop.table(table(datos$partido, datos$voto), margin = 1)
candidato A candidato B
azul 0.90340909 0.09659091
rojo 0.06172840 0.93827160
verde 0.43965517 0.56034483La tabla permite concluir que la gran mayoría de las personas del partido azul (90.3%) votan por el candidato A; la gran mayoría de las personas del partido rojo (93.8%) votan por el cantidado B; y las personas del partido verde distribuyen sus votos de manera similar entre los candidatos.
Finalmente, podemos echar un vistazo a la distribución de edad y su asociación con voto.
ggplot(datos) +
geom_histogram(aes(x = edad), bins = 25, fill = colores[3]) +
labs(x = "Edad", y = "Conteo") +
theme_bw()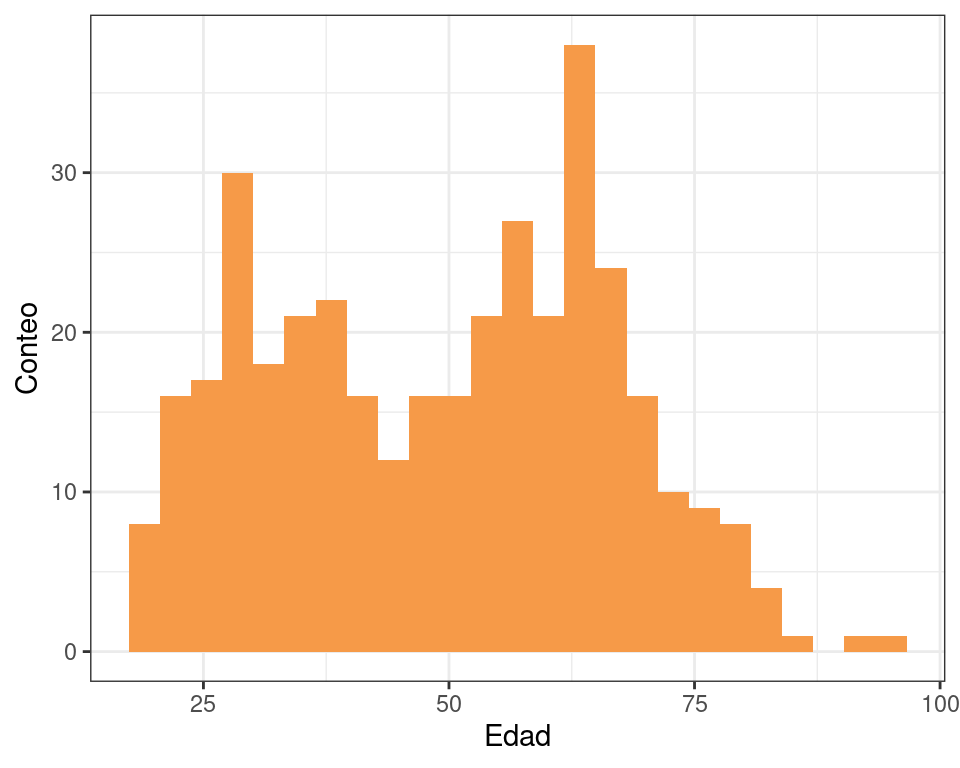
Una manera de ver cómo se asocia la edad con la probabilidad de votar al candidato A es calcular la proporción de personas que votan por el candidato A para diferentes grupos de edad.
# Estos 'breaks' definen los grupos de edad
breaks <- c(18, 30, 40, 60, 80, 95)
prop.table(table(cut(datos$edad, breaks = breaks), datos$voto), margin = 1)
candidato A candidato B
(18,30] 0.6760563 0.3239437
(30,40] 0.6119403 0.3880597
(40,60] 0.5726496 0.4273504
(60,80] 0.5045045 0.4954955
(80,95] 0.4285714 0.5714286A mayor edad, menor proporción de personas votan por el candidato A.
Modelo 1
La implementación del primer modelo en Stan esta la siguiente:
data {
int<lower=1> N; // Cantidad de observaciones
int<lower=0, upper=1> y[N]; // Vector de respuesta (0 y 1)
vector[N] x;
}
parameters {
real a;
real b;
}
model {
// Notar que 'a' y 'b' reciben priors uniformes
y ~ bernoulli_logit(a + b * x);
}Vale la pena destacar el uso de la función bernoulli_logit() que equivale a utilizar una distribución Bernoulli y una función de enlace logit. Esta implementación resulta en un cómputo más estable numéricamente en el caso de modelos de regresión como el nuestro.
stan_data <- list(
N = nrow(datos),
x = datos$edad,
y = as.numeric(datos$voto == "candidato A")
)
ruta_modelo <- here::here("recursos", "codigo", "stan", "elecciones", "modelo_1.stan")
1stan_model <- stan_model(ruta_modelo, auto_write = TRUE)
2stan_fit <- sampling(stan_model, data = stan_data, refresh = 0, seed = 1211)- 1
-
La función
stan_model()crea y compila un modelo de Stan. El argumentoauto_write = TRUEindica que se quiere guardar un archivo.rdsque permite trabajar con el modelo sin tener que volver a compilarlo, resultando en un ahorro de tiempo. - 2
-
sampling()toma el modelo creado porstan_modely los parámetros para muestrear del posterior (los mismos que la funciónstan()usada en otros recursos).
print(stan_fit, pars = c("a", "b"))Inference for Stan model: anon_model.
4 chains, each with iter=2000; warmup=1000; thin=1;
post-warmup draws per chain=1000, total post-warmup draws=4000.
mean se_mean sd 2.5% 25% 50% 75% 97.5% n_eff Rhat
a 1.19 0.01 0.34 0.55 0.95 1.19 1.43 1.84 770 1
b -0.02 0.00 0.01 -0.03 -0.02 -0.02 -0.01 -0.01 782 1
Samples were drawn using NUTS(diag_e) at Thu Jun 13 22:03:58 2024.
For each parameter, n_eff is a crude measure of effective sample size,
and Rhat is the potential scale reduction factor on split chains (at
convergence, Rhat=1).El resumen muestra que los tamaños de muestra efectivos se encuentran cercanos a 800 y la estadística R-hat es igual a 1 para los dos parámetros del modelo.
Antes de seguir analizando el posterior, construyamos un traceplot para evaluar también gráficamente la convergencia y mezcla de las cadenas.
La función spread_draws() de {tidybayes} toma objeto que se obtiene al muestrear el posterior y el nombre de los parámetros de interés y devuelve un data.frame con tantas filas como cantidad de muestras se hayan obtenido.
df_draws <- spread_draws(stan_fit, a, b)
print(nrow(df_draws))[1] 4000head(df_draws)# A tibble: 6 × 5
.chain .iteration .draw a b
<int> <int> <int> <dbl> <dbl>
1 1 1 1 0.816 -0.0113
2 1 2 2 1.03 -0.0138
3 1 3 3 0.844 -0.0101
4 1 4 4 0.743 -0.0144
5 1 5 5 0.831 -0.0132
6 1 6 6 1.02 -0.0131Previo a construir el gráfico necesitamos convertir los datos a formato largo.
df_draws_long <- tidyr::pivot_longer(df_draws, c("a", "b"), names_to = "param")
head(df_draws_long)# A tibble: 6 × 5
.chain .iteration .draw param value
<int> <int> <int> <chr> <dbl>
1 1 1 1 a 0.816
2 1 1 1 b -0.0113
3 1 2 2 a 1.03
4 1 2 2 b -0.0138
5 1 3 3 a 0.844
6 1 3 3 b -0.0101ggplot(df_draws_long) +
geom_line(aes(x = .iteration, y = value, color = as.factor(.chain)), alpha = 0.7) +
scale_color_manual(name = "Cadena", values = colores[1:4]) +
labs(x = "Iteración", y = "Valor") +
facet_wrap(~ param, ncol = 1, scales = "free_y") +
theme_bw()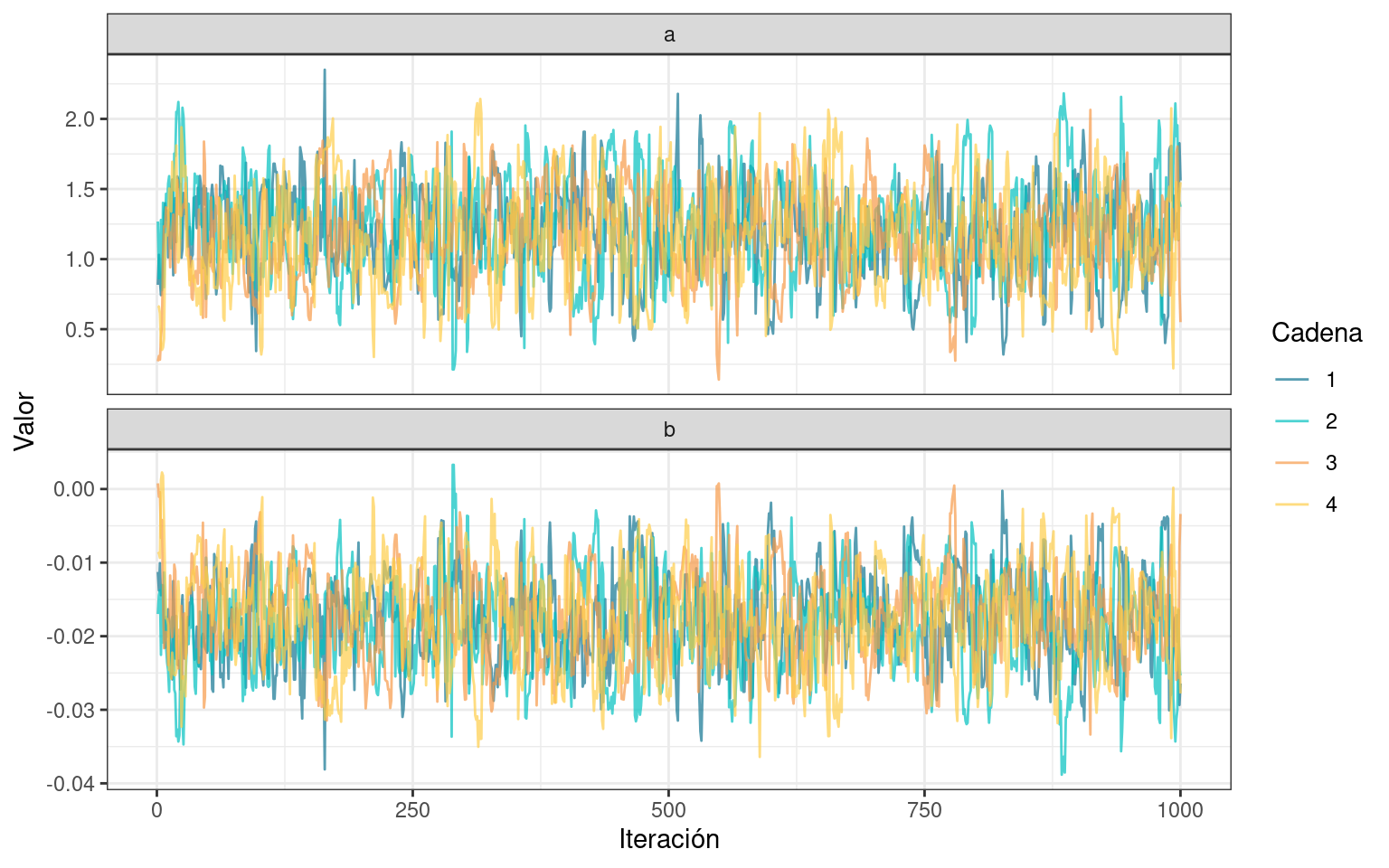
Se puede observar un patrón similar al de un ruido blanco en todos los casos. Las cadenas recorren rangos similares y no presentan tendencias o estancamientos.
El siguiente paso es echar un vistazo a las distribuciones a posteriori marginales.
ggplot(df_draws_long) +
geom_histogram(aes(x = value), bins = 30, fill = colores[3]) +
labs(x = "Valor", y = NULL) +
facet_wrap(~ param, ncol = 2, scales = "free") +
theme_bw() +
theme(axis.ticks.y = element_blank(), axis.text.y = element_blank())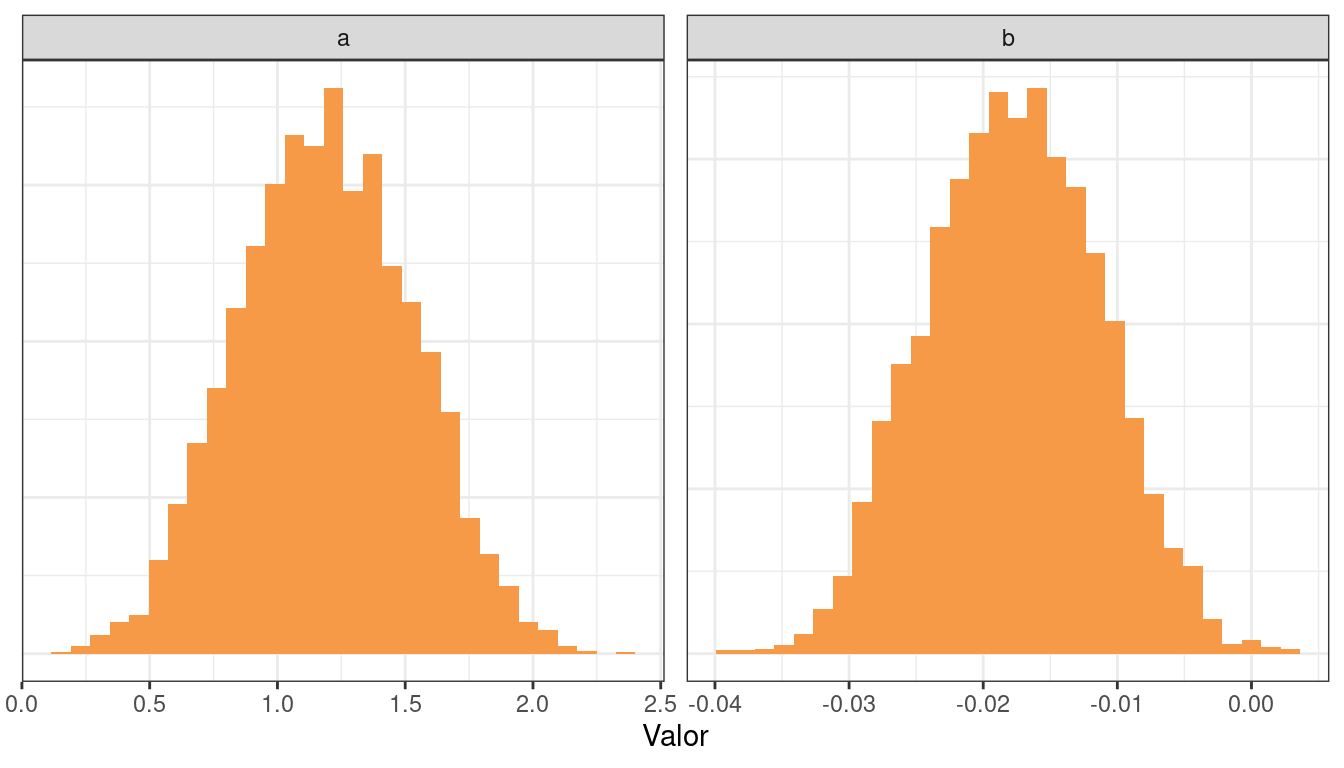
mean(df_draws$b < 0)[1] 0.99725Un dato a resaltar es la asociación negativa entre la edad del votante y la probabilidad de votar por el candidato A. En otras palabras, a mayor edad de la persona, menor la preferencia por el candidato A.
Una forma de interpretar los resultados de manera más amigable es realizar cálculos en términos de probabilidades. Para eso, se utiliza la inversa de la función de enlace:
\[ \text{expit}(x) = \frac{\exp(x)}{1 + \exp(x)} \]
En R, creamos la siguiente función:
expit <- function(x) exp(x) / (1 + exp(x))Esto nos permite observar la distribución a posteriori de la probabilidad de votar al candidato A para, por ejemplo, una persona de 18 años:
1eta_18 <- df_draws$a + df_draws$b * 18
2pi_18 <- expit(eta_18)
data.frame(x = pi_18) |>
ggplot() +
geom_histogram(aes(x = x), fill = colores[3], bins = 30) +
labs(x = "P(Voto = Candidato A | Edad = 18)", y = NULL) +
theme_bw() +
theme(axis.ticks.y = element_blank(), axis.text.y = element_blank())- 1
- Calculamos el predictor lineal para una persona de 18 años.
- 2
- Convertimos el predictor lineal de log-odds a probabilidad.
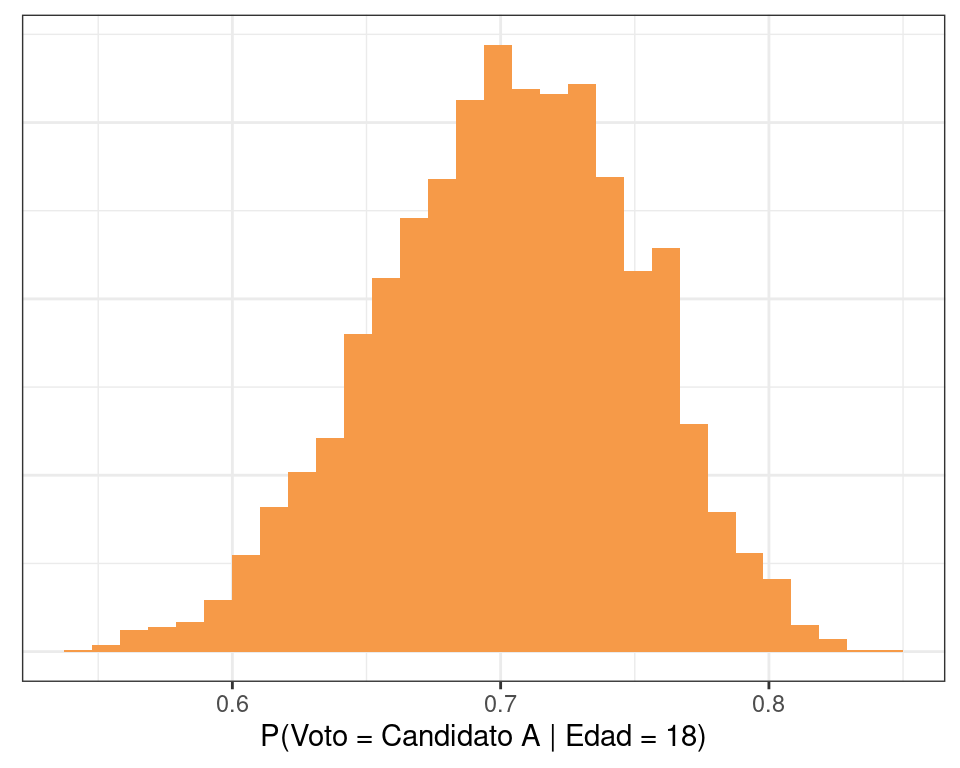
Y también podemos hacer lo mismo para una persona de 50 años.
eta_50 <- df_draws$a + df_draws$b * 50
pi_50 <- expit(eta_50)
data.frame(x = pi_50) |>
ggplot() +
geom_histogram(aes(x = x), fill = colores[3], bins = 30) +
labs(x = "P(Voto = Candidato A | Edad = 50)", y = NULL) +
theme_bw() +
theme(axis.ticks.y = element_blank(), axis.text.y = element_blank())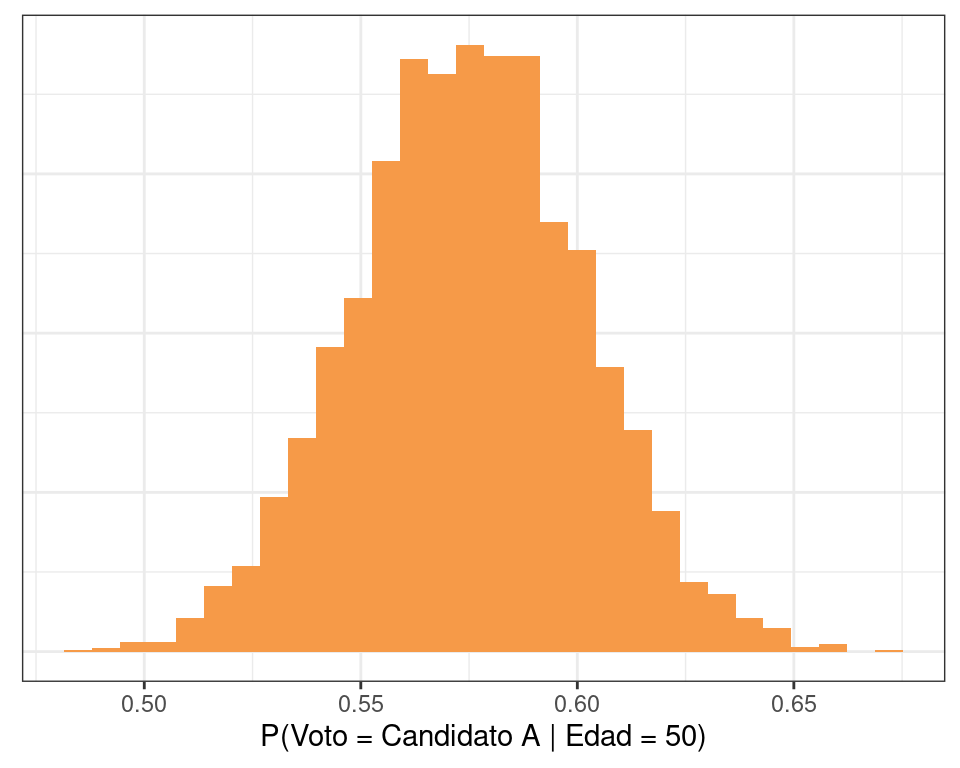
También puede ser de interés visualizar la relación entre la edad (variable explicativa numérica) y el predictor lineal. Debajo construimos el predictor lineal determinado por cada muestra del posterior para edades entre 18 y 95 años.
calcular_eta <- function(pars, x) {
intercepto <- pars[1]
pendiente <- pars[2]
intercepto + pendiente * x
}
n_seq <- 100
n_draws <- 4000
edad_seq <- seq(18, 95, length.out = n_seq)
# (100, 4000)
eta_matrix <- apply(df_draws[c("a", "b")], 1, calcular_eta, x = edad_seq)
df_lines <- data.frame(
eta = as.vector(eta_matrix),
edad = rep(edad_seq, n_draws),
draw = rep(seq_len(n_draws), each = n_seq)
)
head(df_lines) eta edad draw
1 0.6136557 18.00000 1
2 0.6048928 18.77778 1
3 0.5961298 19.55556 1
4 0.5873668 20.33333 1
5 0.5786038 21.11111 1
6 0.5698408 21.88889 1Luego graficamos algunas de ellas:
df_lines |>
filter(draw <= 50) |>
ggplot() +
geom_line(aes(x = edad, y = eta, group = draw), color = "grey20", alpha = 0.7) +
labs(x = "Edad", y = "Predictor lineal") +
theme_bw()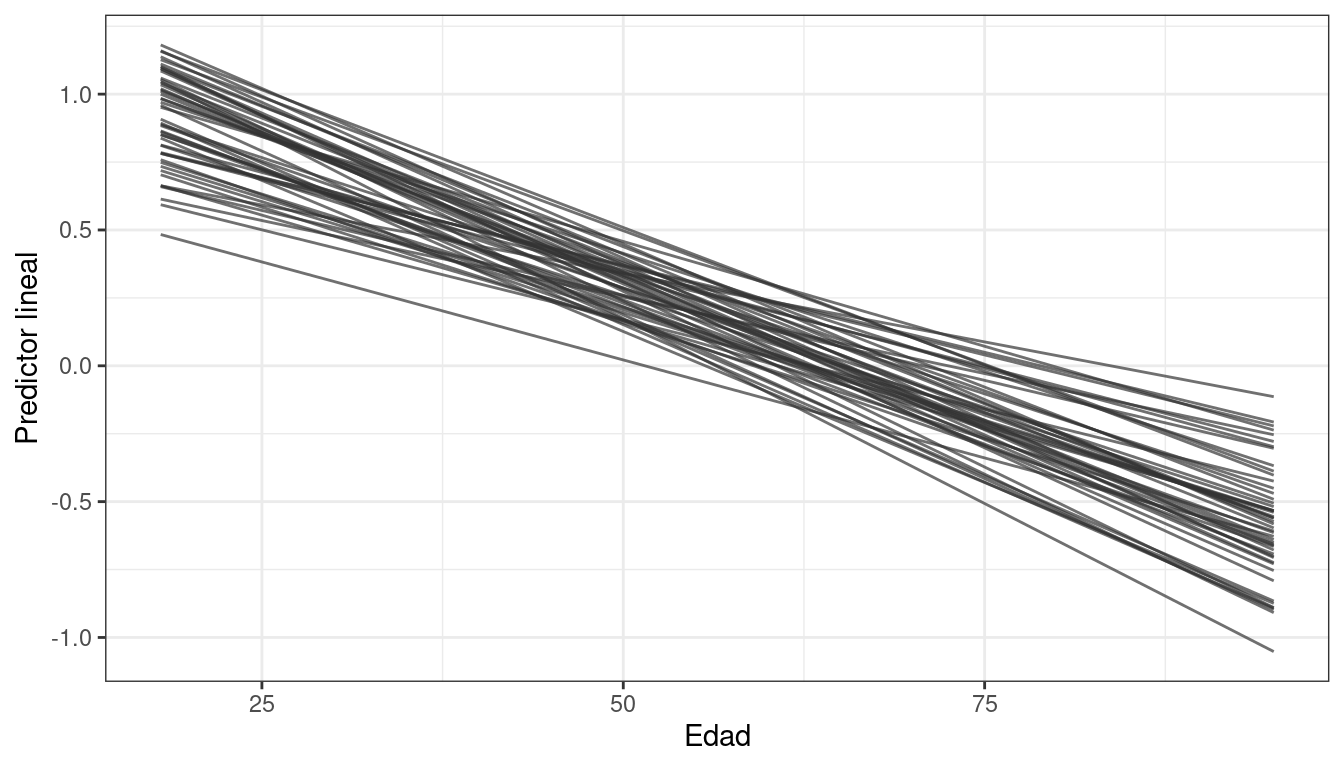
También es posible visualizar la media e intervalos de credibilidad utilizando stat_lineribbon() de {ggdist}. Los intervalos que se muestran son del 50%, 80% y 95%.
df_lines |>
ggplot(aes(x = edad, y = eta)) +
stat_lineribbon(aes(fill_ramp = after_stat(level)), fill = colores[3], color = "grey20") +
labs(x = "Edad", y = "Predictor lineal") +
theme_bw() +
theme(legend.position = "none")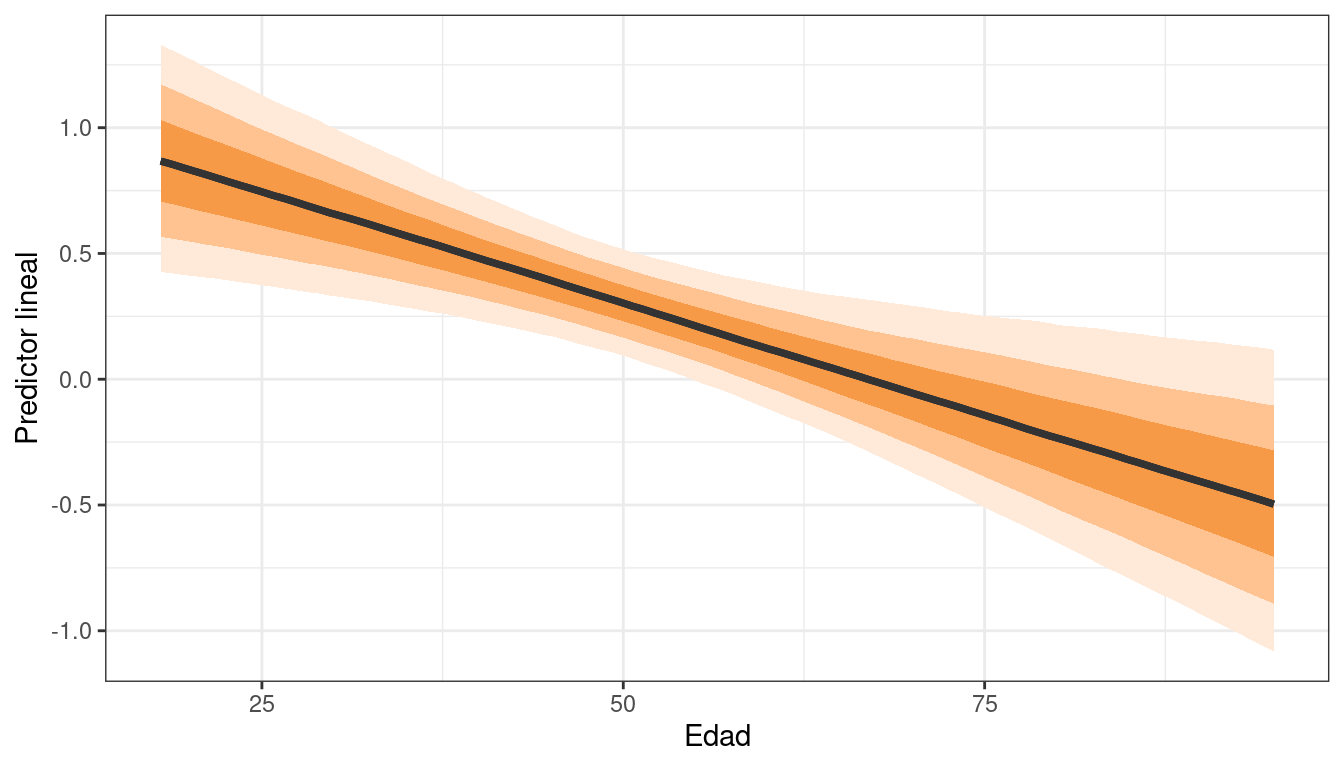
Podemos hacer exactamente lo mismo pero convirtiendo en la escala de las probabilidades.
df_lines |>
filter(draw <= 50) |>
ggplot() +
geom_line(aes(x = edad, y = expit(eta), group = draw), color = "grey20", alpha = 0.7) +
labs(x = "Edad", y = "P(Voto = Candidato A)") +
theme_bw()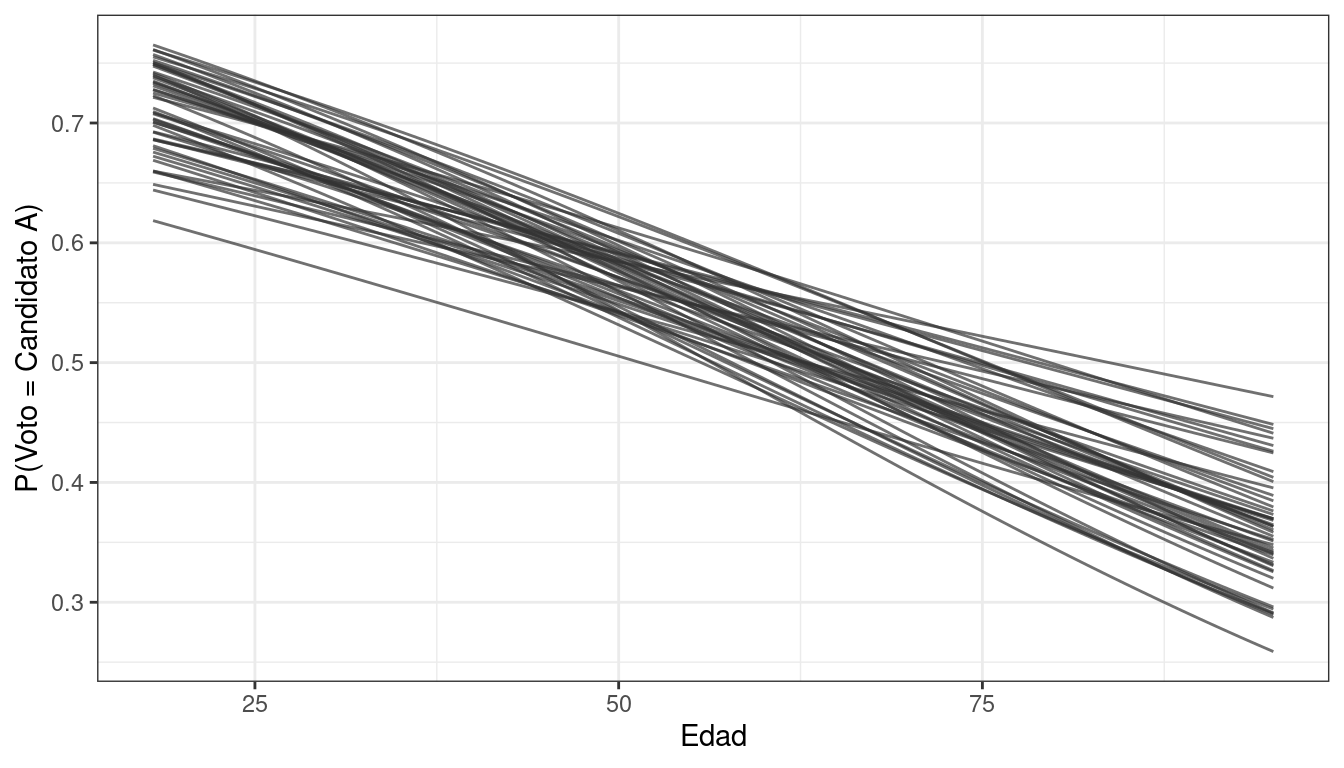
df_lines |>
ggplot(aes(x = edad, y = expit(eta))) +
stat_lineribbon(aes(fill_ramp = after_stat(level)), fill = colores[3], color = "grey20") +
labs(x = "Edad", y = "P(Voto = Candidato A)") +
theme_bw() +
theme(legend.position = "none")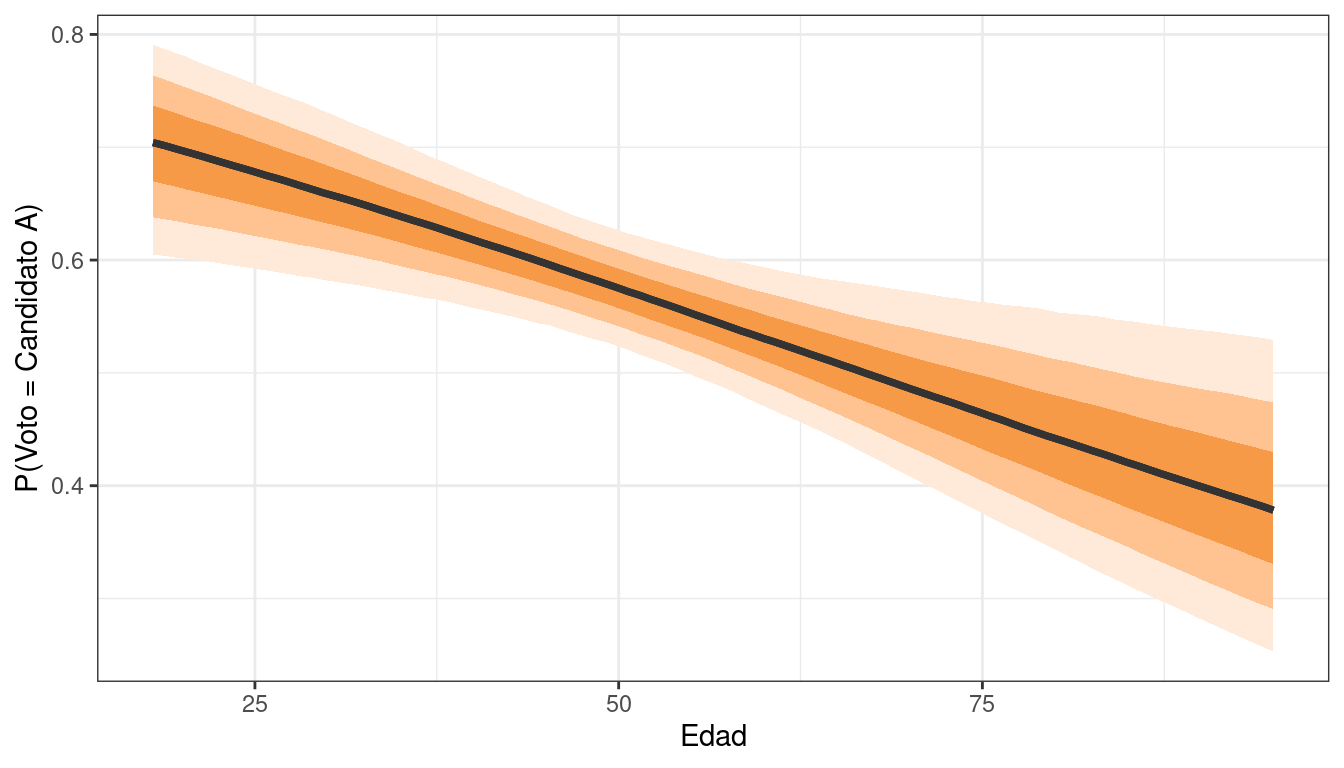
La edad se asocia negativamente con la probabilidad de votar por el candidato A. Si analizamos los extremos podemos ver que:
- Las personas de 18 años tienen una probabilidad de entre el 60% y el 80% de votar por el candidato A.
- Las personas de 95 años tienen una probabilidad de entre el 25% y el 50% de votar por el candidato A.
Modelo 2
La implementación del primer modelo en Stan esta la siguiente:
data {
int<lower=1> N; // Cantidad de observaciones
int<lower=0, upper=1> y[N]; // Vector de respuesta (0 y 1)
int partido_idx[N]; // Índice del partido
vector[N] x;
}
parameters {
vector[3] a;
vector[3] b;
}
model {
y ~ bernoulli_logit(a[partido_idx] + b[partido_idx] .* x);
}La principal diferencia con el modelo 1 es que ahora los parámetros son vectores, ya que se tienen tantos interceptos y pendientes como partidos políticos.
as.factor(datos$partido)[1:10] [1] azul rojo azul rojo rojo azul azul verde azul azul
Levels: azul rojo verdestan_data <- list(
N = nrow(datos),
x = datos$edad,
y = as.numeric(datos$voto == "candidato A"),
partido_idx = as.numeric(as.factor(datos$partido))
)
ruta_modelo <- here::here("recursos", "codigo", "stan", "elecciones", "modelo_2.stan")
stan_model <- stan_model(ruta_modelo, auto_write = TRUE)
stan_fit <- sampling(stan_model, data = stan_data, refresh = 0, seed = 1211)print(stan_fit, pars = c("a", "b"))Inference for Stan model: anon_model.
4 chains, each with iter=2000; warmup=1000; thin=1;
post-warmup draws per chain=1000, total post-warmup draws=4000.
mean se_mean sd 2.5% 25% 50% 75% 97.5% n_eff Rhat
a[1] 1.71 0.01 0.72 0.37 1.22 1.69 2.17 3.22 2537 1
a[2] 0.92 0.03 1.59 -2.07 -0.17 0.88 1.99 4.20 2502 1
a[3] 1.43 0.01 0.63 0.22 1.01 1.42 1.84 2.68 1967 1
b[1] 0.01 0.00 0.02 -0.02 0.00 0.01 0.02 0.04 2378 1
b[2] -0.09 0.00 0.04 -0.19 -0.12 -0.09 -0.06 -0.02 2305 1
b[3] -0.03 0.00 0.01 -0.06 -0.04 -0.03 -0.03 -0.01 1976 1
Samples were drawn using NUTS(diag_e) at Thu Jun 13 22:05:10 2024.
For each parameter, n_eff is a crude measure of effective sample size,
and Rhat is the potential scale reduction factor on split chains (at
convergence, Rhat=1).En este segundo modelo tenemos que los tamaños de muestra efectivo son sustancialmente mayores que en el primer modelo (entre 2000 y 2500) y que nuevamente los R-hat son iguales a 1.
A la hora de usar spread_draws hay que tener en cuenta que los parámetros están indexados por partido_idx.
df_draws <- spread_draws(stan_fit, a[partido_idx], b[partido_idx])
head(df_draws)# A tibble: 6 × 6
# Groups: partido_idx [1]
partido_idx a .chain .iteration .draw b
<int> <dbl> <int> <int> <int> <dbl>
1 1 2.19 1 1 1 0.0119
2 1 1.64 1 2 2 0.00267
3 1 2.73 1 3 3 0.00188
4 1 2.20 1 4 4 -0.00796
5 1 2.58 1 5 5 0.00468
6 1 4.17 1 6 6 -0.0241 df_draws_long <- tidyr::pivot_longer(df_draws, c("a", "b"))
df_draws_long <- df_draws_long |>
dplyr::mutate(
parametro = ifelse(name == "a", "intercepto", "pendiente"),
partido = case_when(
partido_idx == 1 ~ "azul",
partido_idx == 2 ~ "rojo",
partido_idx == 3 ~ "verde",
)
)
head(df_draws_long)# A tibble: 6 × 8
# Groups: partido_idx [1]
partido_idx .chain .iteration .draw name value parametro partido
<int> <int> <int> <int> <chr> <dbl> <chr> <chr>
1 1 1 1 1 a 2.19 intercepto azul
2 1 1 1 1 b 0.0119 pendiente azul
3 1 1 2 2 a 1.64 intercepto azul
4 1 1 2 2 b 0.00267 pendiente azul
5 1 1 3 3 a 2.73 intercepto azul
6 1 1 3 3 b 0.00188 pendiente azul ggplot(df_draws_long) +
geom_line(
aes(x = .iteration, y = value, color = as.factor(.chain)),
alpha = 0.7
) +
scale_color_manual(name = "Cadena", values = colores[1:4]) +
labs(x = "Iteración", y = "Valor") +
facet_wrap(vars(parametro, partido), nrow = 6, scales = "free", labeller = label_both) +
theme_bw()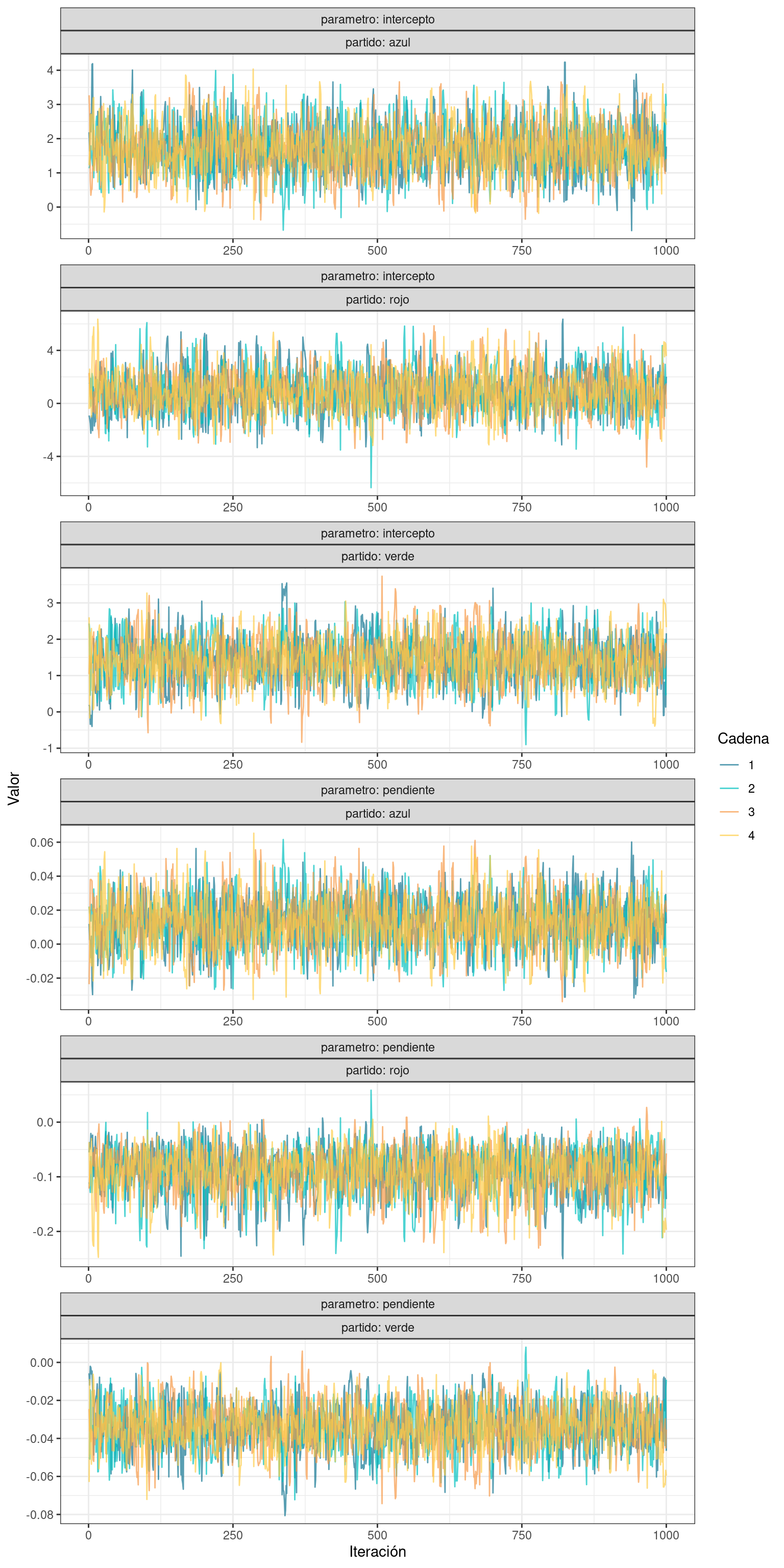
Gráficamente, se vuelve a observar un patrón similar al ruido blanco en todos los casos, y que las cadenas se mezclan y recorren los mismos intervalos del espacio paramétrico.
Para las distribuciones marginales del posterior podemos construir la siguiente visualización:
df_draws_long |>
ggplot() +
geom_histogram(aes(x = value), bins = 50, fill = colores[3]) +
labs(x = "Valor", y = NULL) +
facet_grid(vars(partido), vars(parametro), labeller = label_both, scales = "free_x") +
theme_bw() +
theme(axis.ticks.y = element_blank(), axis.text.y = element_blank())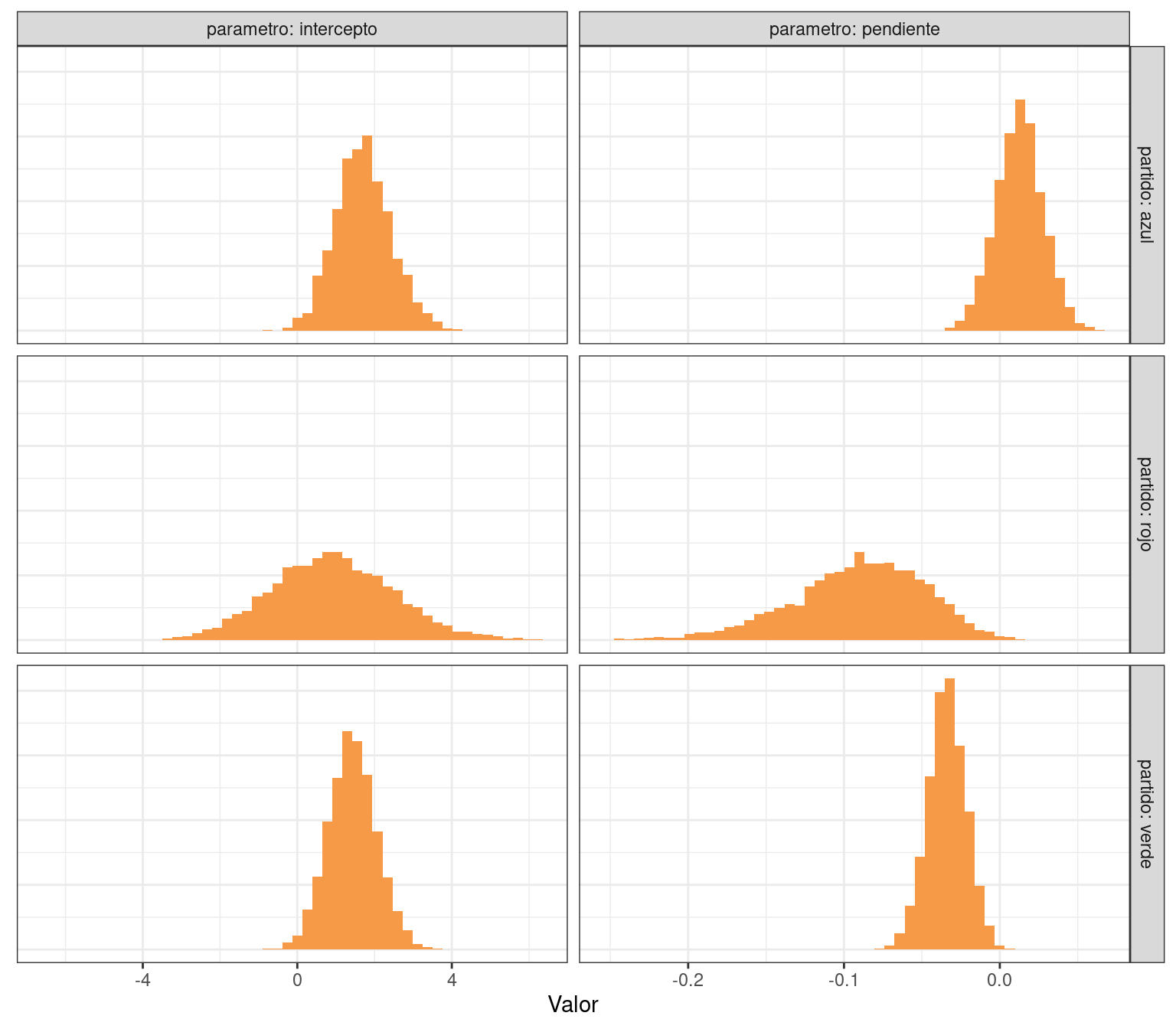
Los interceptos no parecen ser distintos, y la pendiente del partido azul parece ser mayor que la del resto. Sin embargo, para llegar a estas conclusiones es necesario utilizar las distribuciones conjuntas, lo cual haremos hacia el final de este recurso.
A partir del modelo 2, se obtienen diferentes predictores lineales según el partido que podemos visualizar a continuación:
n_seq <- 100
n_draws <- 4000
edad_seq <- seq(18, 95, length.out = n_seq)
# (100, 12000)
eta_matrix <- apply(df_draws[c("a", "b")], 1, calcular_eta, x = edad_seq)
df_lines <- data.frame(
eta = as.vector(eta_matrix), # 1,200,000
edad = rep(edad_seq, n_draws * 3),
draw = rep(rep(seq_len(n_draws), each = n_seq), 3),
partido_idx = rep(df_draws$partido_idx, each = n_seq)
)
df_lines <- df_lines |>
mutate(
partido = case_when(
partido_idx == 1 ~ "azul",
partido_idx == 2 ~ "rojo",
partido_idx == 3 ~ "verde",
)
)
head(df_lines) eta edad draw partido_idx partido
1 2.400951 18.00000 1 1 azul
2 2.410211 18.77778 1 1 azul
3 2.419472 19.55556 1 1 azul
4 2.428733 20.33333 1 1 azul
5 2.437993 21.11111 1 1 azul
6 2.447254 21.88889 1 1 azuldf_lines |>
filter(draw <= 50) |>
ggplot() +
geom_line(aes(x = edad, y = eta, group = draw), color = "grey20", alpha = 0.7) +
labs(x = "Edad", y = "Predictor lineal") +
facet_wrap(~ partido, ncol = 3, labeller = label_both) +
theme_bw()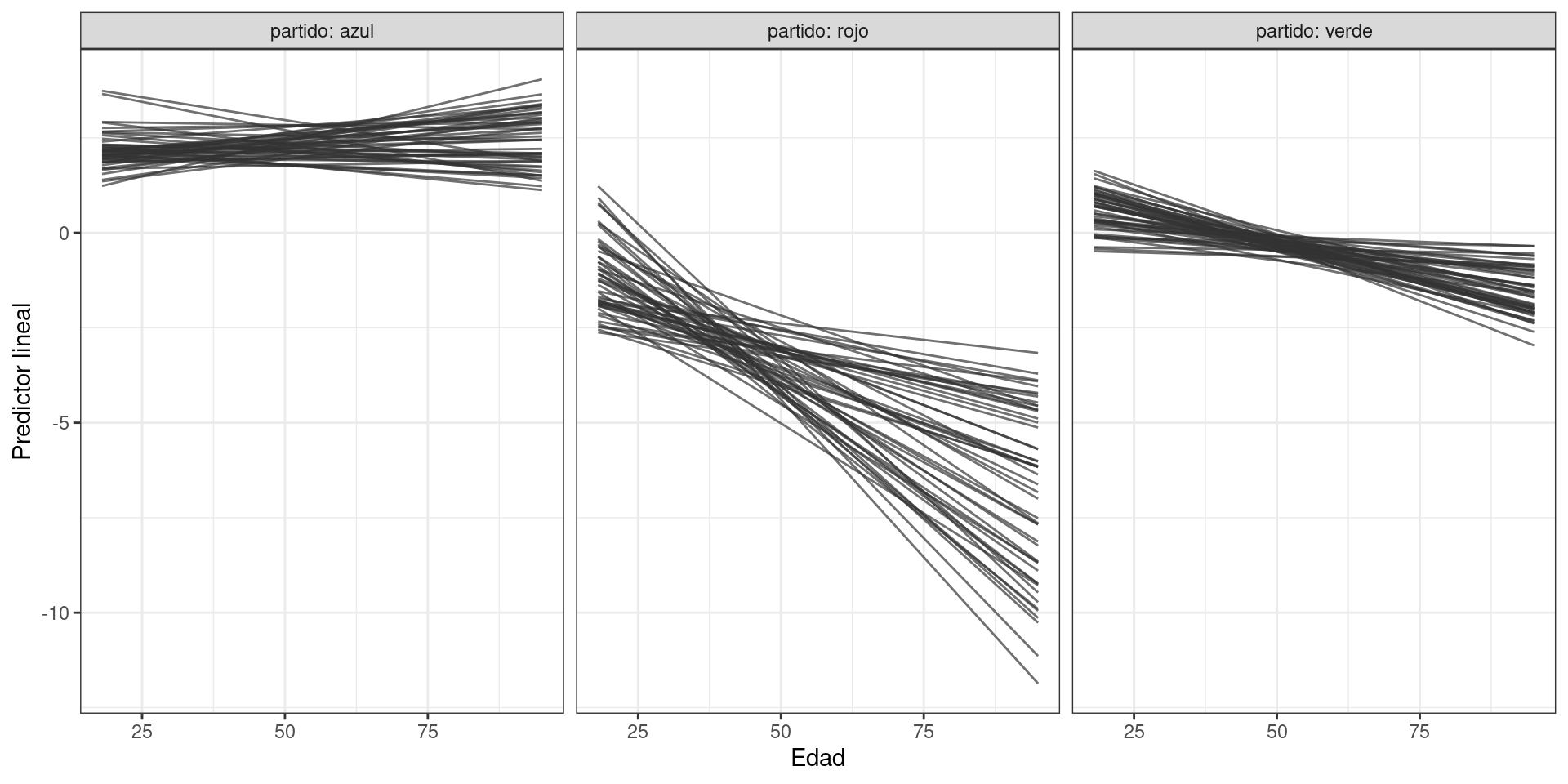
En la visualización debajo graficamos cómo evoluciona la probabilidad de votar por el candidato A según la edad y la identificación política. Para eso, seleccionamos algunas muestras del posterior y trazamos las curvas que estas implican. Los colores identifican a los partidos.
df_lines |>
filter(draw <= 50) |>
ggplot() +
geom_line(aes(x = edad, y = expit(eta), group = interaction(draw, partido), color = partido)) +
scale_color_manual(values = c("#3498db", "#e74c3c","#2ecc71")) +
labs(x = "Edad", y = "P(Voto = Candidato A)") +
theme_bw() +
theme(legend.position = "none")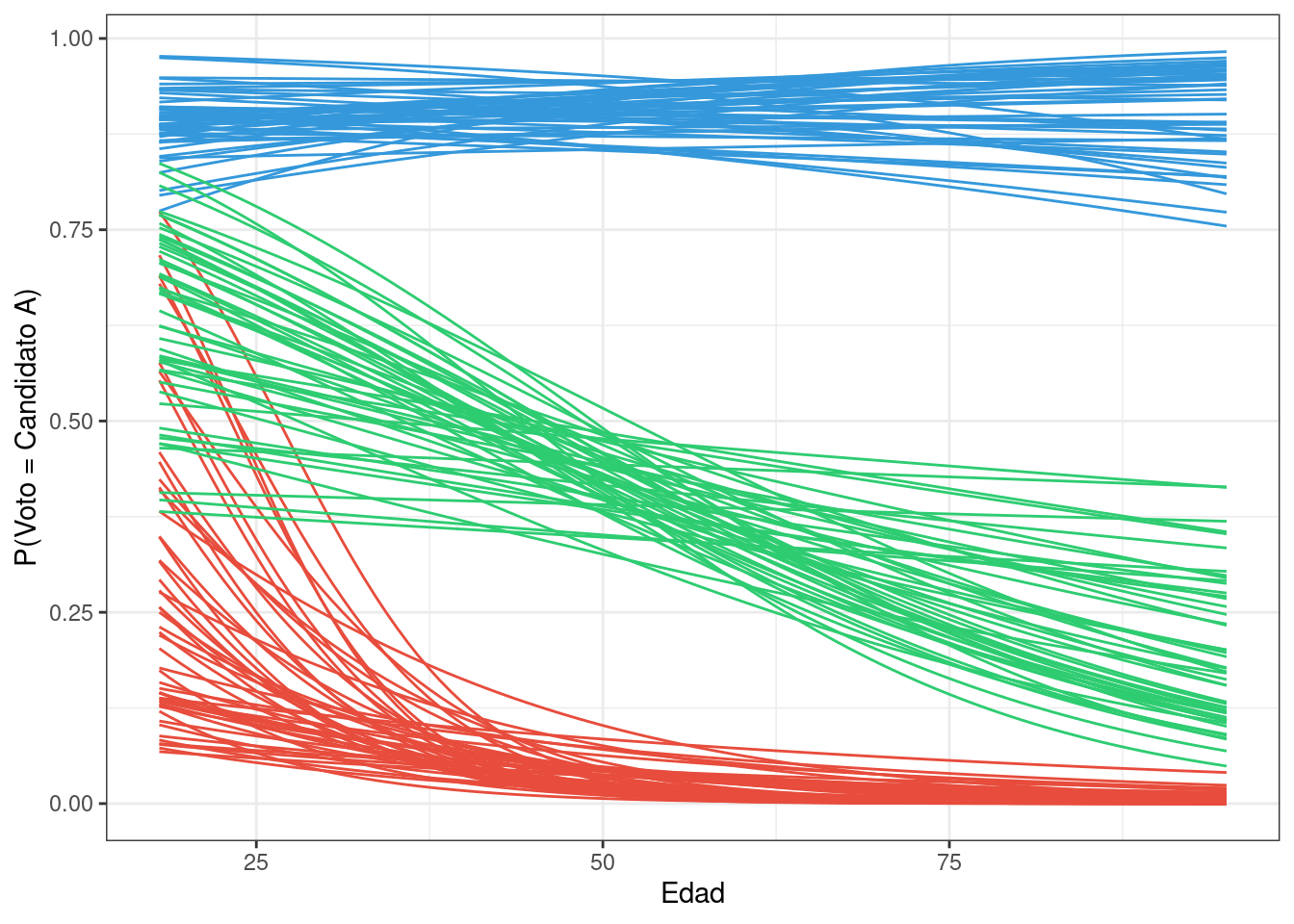
De manera análoga, podemos obtener una visualización usando todas las muestras del posterior en base a stat_linerribon().
df_lines |>
ggplot(aes(x = edad, y = expit(eta), fill = partido)) +
stat_lineribbon(aes(fill_ramp = after_stat(level)), color = "grey20") +
scale_fill_manual(values = c("#3498db", "#e74c3c","#2ecc71")) +
labs(x = "Edad", y = "P(Voto = Candidato A)") +
theme_bw() +
theme(legend.position = "none")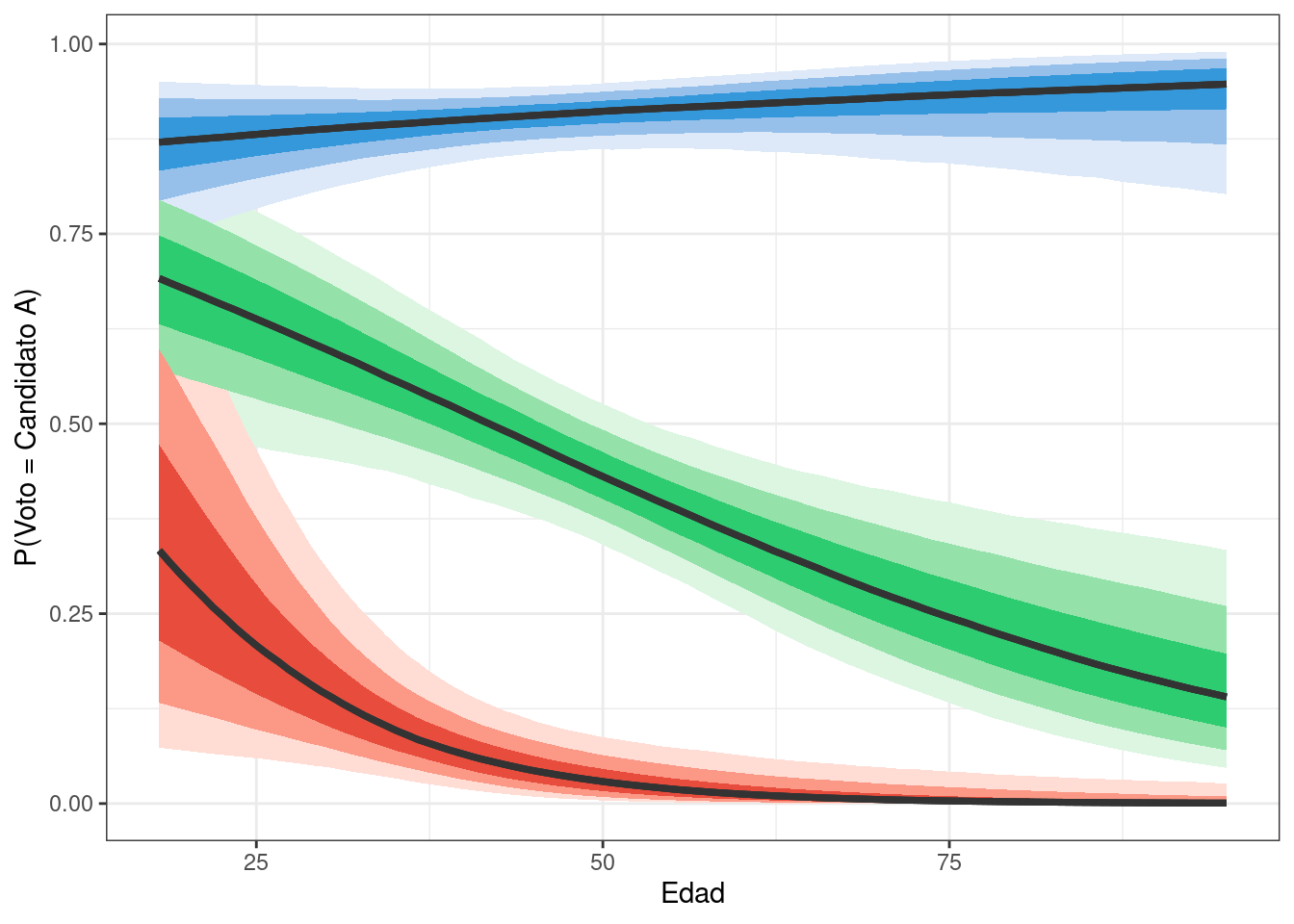
Según nuestro modelo de regresión logística, la probabilidad media de votar por el candidato A para los del partido azul es siempre elevada (superior a 0.8), sin importar la edad. Además, cuanto mayor es la persona, más cercana a 1 es la probabilidad media de votar por el candidato A.
Por otro lado, si bien los del partido rojo tienen una probabilidad no nula de votar por el candidato A cuando son jóvenes, ésta tiende a cero rápidamente cuando se incrementa la edad.s También podemos notar una alta variabilidad en la probabilidad de votar al candidato A para los jóvenes del partido rojo. Esto refleja una gran incertidumbre al estimar esta probabilidad y se debe a la pequeña cantidad de personas del partido rojo en ese rango de edad, además de que solo 5 de los 97 del partido rojo en el conjunto de datos votan por el candidato A.
Finalmente, la probabilidad media de votar por el candidato A para los del partido verde es de alrededor de 0.7 para los más jóvenes y disminuye hacia 0.2 a medida que envejecen. Dado que la dispersión de las líneas es similar a lo largo de todas las edades, podemos concluir que nuestra incertidumbre en esta estimación es similar para todos los grupos de edad.
Ahora, utilizando el posterior conjunto, podemos responder nuestras preguntas en términos de probabilidades.
¿Cuál es la probabilidad de que la pendiente del partido azul sea mayor que la pendiente del partido rojo?
mean(df_draws[df_draws$partido_idx == 1, "b"] > df_draws[df_draws$partido_idx == 2, "b"])[1] 0.9945¿Cuál es la probabilidad de que la pendiente del partido azul sea mayor que la pendiente del partido verde?
mean(df_draws[df_draws$partido_idx == 1, "b"] > df_draws[df_draws$partido_idx == 3, "b"])[1] 0.99075¿Cuál es la probabilidad de que la pendiente del partido rojo sea mayor que la pendiente del partido verde?
mean(df_draws[df_draws$partido_idx == 2, "b"] > df_draws[df_draws$partido_idx == 3, "b"])[1] 0.08425¿Cuál es la probabilidad de que la pendiente del partido azul sea positiva?
mean(df_draws[df_draws$partido_idx == 1, "b"] > 0)[1] 0.7965¿Cuál es la probabilidad de que la pendiente del partido rojo sea negativa?
mean(df_draws[df_draws$partido_idx == 2, "b"] < 0)[1] 0.995¿Cuál es la probabilidad de que la pendiente del partido verde sea negativa?
mean(df_draws[df_draws$partido_idx == 3, "b"] < 0)[1] 0.99875