05 - Propiedades frecuentistas de inferencias bayesianas

El siguiente programa sirve para responder al ejercicio Propiedades frecuentistas de inferencias bayesianas de la Práctica 2.

library(ggplot2)

set.seed(1234)

# Definir cantidad de repeticiones
reps_n <- 10000

# Definir valores de 'n'
n_vector <- c(1, 5, 10, 25)

# Definir valores de 'theta'
theta_vector <- seq(0.05, 0.5, by = 0.05)

# Definir hiperparámetros del prior
a_prior <- 0.5
b_prior <- 0.5

# Crear matriz para almacenar las coberturas empíricas
coberturas <- matrix(
    nrow = length(n_vector),
    ncol = length(theta_vector)
)

for (i in seq_along(n_vector)) {
    for (j in seq_along(theta_vector)) {
        n <- n_vector[i]
        theta <- theta_vector[j]
        y_rvs <- rbinom(reps_n, n, theta)
        a_posterior <- a_prior + y_rvs
        b_posterior <- b_prior + (n - y_rvs)
        ic_lower <- qbeta(0.025, a_posterior, b_posterior)
        ic_upper <- qbeta(0.975, a_posterior, b_posterior)
        cobertura <- mean(theta > ic_lower & theta < ic_upper)
        cat("n=", n, "theta=", theta, "cobertura=", cobertura, "\n")
        coberturas[i, j] <- cobertura
    }
}

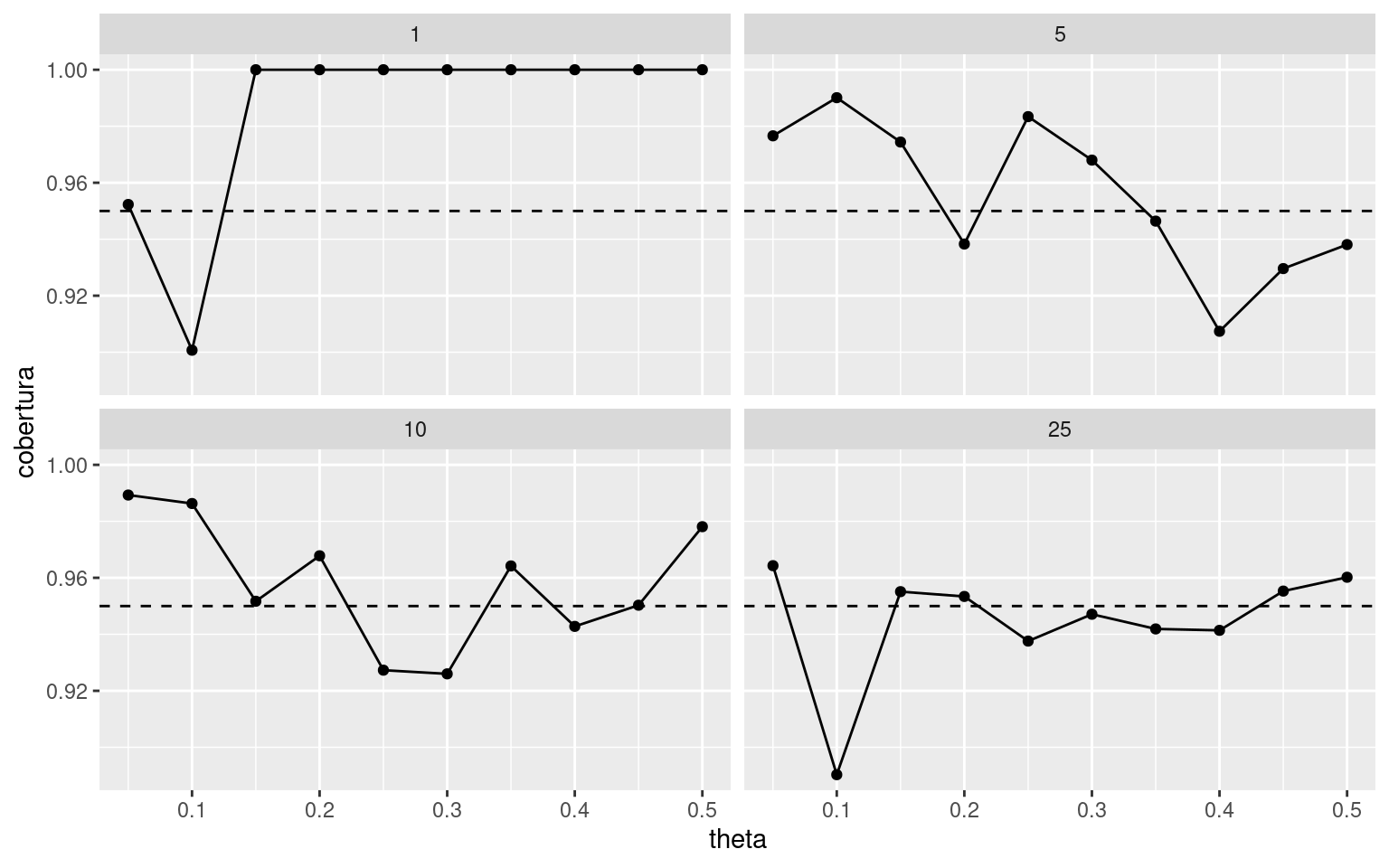
n= 1 theta= 0.05 cobertura= 0.9523 
n= 1 theta= 0.1 cobertura= 0.9007 
n= 1 theta= 0.15 cobertura= 1 
n= 1 theta= 0.2 cobertura= 1 
n= 1 theta= 0.25 cobertura= 1 
n= 1 theta= 0.3 cobertura= 1 
n= 1 theta= 0.35 cobertura= 1 
n= 1 theta= 0.4 cobertura= 1 
n= 1 theta= 0.45 cobertura= 1 
n= 1 theta= 0.5 cobertura= 1 
n= 5 theta= 0.05 cobertura= 0.9766 
n= 5 theta= 0.1 cobertura= 0.9901 
n= 5 theta= 0.15 cobertura= 0.9744 
n= 5 theta= 0.2 cobertura= 0.9383 
n= 5 theta= 0.25 cobertura= 0.9834 
n= 5 theta= 0.3 cobertura= 0.968 
n= 5 theta= 0.35 cobertura= 0.9464 
n= 5 theta= 0.4 cobertura= 0.9074 
n= 5 theta= 0.45 cobertura= 0.9296 
n= 5 theta= 0.5 cobertura= 0.9381 
n= 10 theta= 0.05 cobertura= 0.9893 
n= 10 theta= 0.1 cobertura= 0.9863 
n= 10 theta= 0.15 cobertura= 0.9517 
n= 10 theta= 0.2 cobertura= 0.9678 
n= 10 theta= 0.25 cobertura= 0.9273 
n= 10 theta= 0.3 cobertura= 0.926 
n= 10 theta= 0.35 cobertura= 0.9642 
n= 10 theta= 0.4 cobertura= 0.9428 
n= 10 theta= 0.45 cobertura= 0.9503 
n= 10 theta= 0.5 cobertura= 0.9781 
n= 25 theta= 0.05 cobertura= 0.9643 
n= 25 theta= 0.1 cobertura= 0.8903 
n= 25 theta= 0.15 cobertura= 0.9551 
n= 25 theta= 0.2 cobertura= 0.9534 
n= 25 theta= 0.25 cobertura= 0.9376 
n= 25 theta= 0.3 cobertura= 0.9471 
n= 25 theta= 0.35 cobertura= 0.9419 
n= 25 theta= 0.4 cobertura= 0.9414 
n= 25 theta= 0.45 cobertura= 0.9553 
n= 25 theta= 0.5 cobertura= 0.9602 

# Crear combinaciones entre los valores de 'n' y 'theta'
datos <- as.data.frame(expand.grid(n_vector, theta_vector))

# Asignar nombres de columnas mas claros
colnames(datos) <- c("n", "theta")

# Transformar matriz en vector y guardar como columna del data frame
datos$cobertura <- as.vector(coberturas)

# Graficar con ggplot2
ggplot(datos, aes(x = theta, y = cobertura)) +
    geom_line() +
    geom_point() +
    geom_hline(yintercept = 0.95, linetype = "dashed") +
    facet_wrap(~ as.factor(n))